6.
5°.. 6°..
Теория.
Решение показательных и логарифмических уравнений и неравенств.
Основные свойства и графики.
Степенная, показательная, логарифмическая функции.
5.
Свойства операции возведения в степень:
1°. 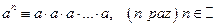 . 2°.
. 2°. 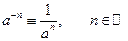 .
.
3°. 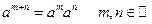 . 4°.
. 4°. 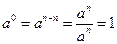 .
.
Свойства операции нахождения логарифма:
0°. Основное логарифмическое тождество: 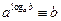 . Свойство является, по сути дела, оп-
. Свойство является, по сути дела, оп-
ределением операции логарифмирования.
1°. 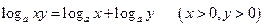 . 2°.
. 2°. 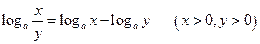 .
.
3°. 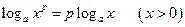 . 4°.
. 4°. 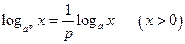 .
.
5°. 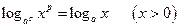 . 6°.
. 6°. 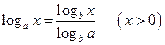 .
.
Показательной функцией называется функция 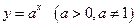 .
.
 Ее свойства:
Ее свойства:
1. Область определения 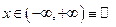 .
.
2. Область значений 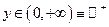 .
.
3. 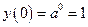 .
.
4. 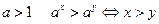 ,
,
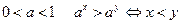 .
.
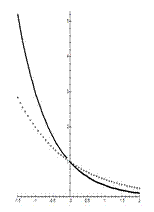
На приведенных рисунках видим графики показательных функций с различными основаниями: слева – с основаниями 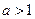 , справа – с основаниями
, справа – с основаниями 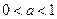 .
.
При этом, сплошной линией изображены графики показательной функции с основаниями 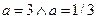 , а крестиками – с основаниями
, а крестиками – с основаниями 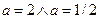 .
.
Показательная функция определена для любых вещественных значениях показателя степени и принимает только положительные значения, что и указано в свойствах 1 и 2 показательной функции. Графики всех показательных функций проходят через точку с координатами 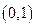 (свойство 3).
(свойство 3).
Свойство 4 показательной функции говорит о том, что при основаниях больших единицы показательная функция есть функция возрастающая, а при основаниях меньших единицы – убывающая.
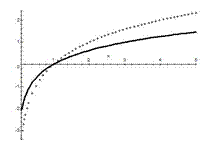 Логарифмической функцией называется функция вида
Логарифмической функцией называется функция вида
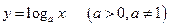 , являющаяся функцией обратной показательной функции с тем же основанием.
, являющаяся функцией обратной показательной функции с тем же основанием.
Свойства логарифмической функции:
1. Область определения 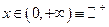 .
.
2. Область значений 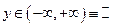 .
.
3. 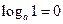 .
.
 4.
4. 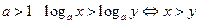 ,
,
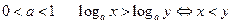 .
.
Свойства 1 и 2 показывают, что область определения и область значений показательной функции для логарифмической функции поменялись местами, что и естественно ибо это взаимно обратные функции.
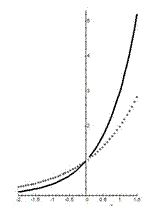
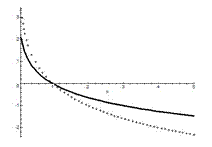
Графики всех логарифмических функций проходят через точку с координатами 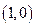 (свойство 3).
(свойство 3).
Свойство 4 показательной функции указывает на то, что при основаниях больших единицы логарифмическая функция есть функция возрастающая, а при основаниях меньших единицы – убывающая.
На приведенных рисунках видим графики логарифмических функций с различными основаниями: сверху – с основаниями 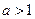 , снизу – с основаниями
, снизу – с основаниями 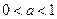 .
.
При этом, сплошной линией изображены графики логарифмической функции с основаниями 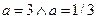 , а крестиками – с основаниями
, а крестиками – с основаниями 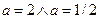 .
.
И, наконец:
Общая схема решения показательных и логарифмических уравнений и неравенств.
1. Переход к одному и тому же основанию во всех показательных (логарифмических)функциях, входящих в данное уравнение.
2. Переход к одному и тому же показателю степени (выражению под знаком логарифма).
3. Замена показательной (логарифмической) функции новой переменной.
4. Решение получившегося уравнения или неравенства относительно новой переменной.
5. Обратная замена и возврат к показательным (логарифмическим) функциям.
6. Решение простейших показательных (логарифмических)уравнений или неравенств.
Задачи для решения:1*, 2*, …, 24*
Решить следующие показательные неравенства:
1*. 25– х + 5– х +1 ³ 50; 2*. 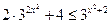 ;
;
3*. 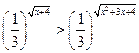 ; 4*. 98 –
; 4*. 98 – 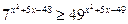 ;
;
5*. 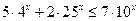 ; 6*.
; 6*. 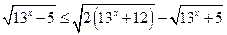 ;
;
7*. 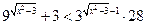 ; 8*.
; 8*. 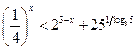 ;
;
9*. 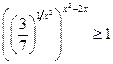 ; 10*.
; 10*. 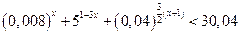 ;
;
11*. 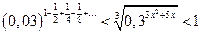 ; 12*.
; 12*. 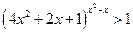 ;
;
13*. 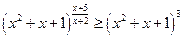 ;
;
Решить следующие логарифмические неравенства:
14*. 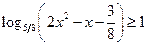 ; 15*.
; 15*. 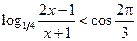 ;
;
16*. 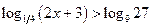 ; 17*.
; 17*. 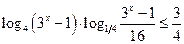 ;
;
18*. 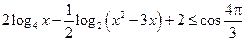 ;
;
19*. 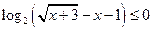 ; 20*.
; 20*. 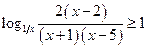 ;
;
21*. 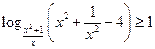 ; 22*.
; 22*. 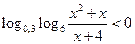 ;
;
23*. 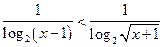 ; 24*.
; 24*. 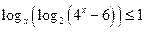 .
.
 2014-02-24
2014-02-24 710
710








