Произвольная система линейных уравнений называется совместной, если она имеет решения, и не совместной в противном случае. При этом совместная система линейных уравнений называется определенной, если она имеет единственное решение, и не определенной если она имеет более одного (а именно бесконечно много) решений.
Для системы двух линейных уравнений с двумя неизвестными исследование на совместность производится очень просто.
Если задана система 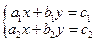 , то:
, то:
а) если 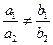 , то система совместна и определена, т.е. имеет единственное решение;
, то система совместна и определена, т.е. имеет единственное решение;
б) если 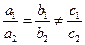 , то система не совместна, т.е. не имеет решений;
, то система не совместна, т.е. не имеет решений;
в) если 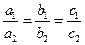 , то система совместна и не определена, т.е. имеет бесконечно много решений;
, то система совместна и не определена, т.е. имеет бесконечно много решений;
Для систем линейных уравнений с количеством неизвестных более двух исследование на совместность более сложно и будет изучено позднее.
Основным методом решения систем линейных уравнений является метод Гаусса исключения неизвестных, который, при некоторой модификации, позволяет как исследовать систему на совместность – не совместность, так и, в случае совместности, найти решения как определенных так и не определенных систем.
Задачи для решения:1*, 2*, …, 15*
Исследовать на совместность и решить системы линейных уравнений с двумя неизвестными:
1*. 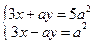 ; 2*.
; 2*. 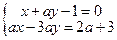 ;
;
3*. 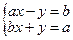 ; 4*.
; 4*. 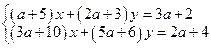 ;
;
5*. 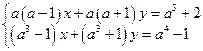 ;
;
6*. 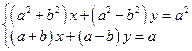 .
.
7*. Числа a и b таковы, что система 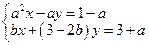 имеет единственное решение х = 1, у = 1. Найти a и b.
имеет единственное решение х = 1, у = 1. Найти a и b.
8*. При каких a и b система 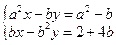 имеет бесконечно много решений?
имеет бесконечно много решений?
9*. При каких a система 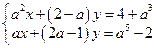 не имеет решений?
не имеет решений?
10*. Числа a, b и с таковы, что система
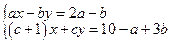 имеет бесконечно много решений,
имеет бесконечно много решений,
причем х = 1, у = 3, одно из них. Найти a и b.
11*. Найти все такие значения а, чтобы при любом b, нашлось такие с при которых система имеет хотя бы одно решение:
а) 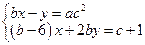 ; б)
; б) 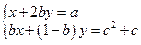 .
.
Решить системы линейных уравнений методом Гаусса исключения неизвестных:
12*. 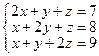 ; 13*.
; 13*. 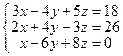 ;
;
14*. 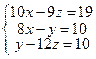 ; 15*.
; 15*. 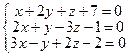 .
.
 2014-02-24
2014-02-24 970
970








