3.
Теория
2.
Свойства функции y = ax 2 + bx + c. Квадратные уравнения и задачи связанные с исследованием квадратичных функций.
Формулы для запоминания:
Для уравнения 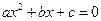 :
: 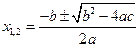 ,если
,если 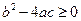 .
.
Для уравнения 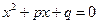 :
: 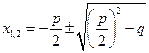 ,если
,если 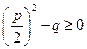 .
.
Выражение 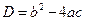 называется дискриминантом квадратного уравнения и его знак определяет количество вещественных корней квадратного уравнения.
называется дискриминантом квадратного уравнения и его знак определяет количество вещественных корней квадратного уравнения.
Т°.(Виета). Для квадратного уравнения 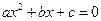 , имеющего корни
, имеющего корни 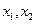 выполняются соотношения:
выполняются соотношения: 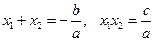 . Для приведенного квадратного уравнения
. Для приведенного квадратного уравнения 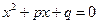 , имеющего корни
, имеющего корни 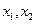 выполняются соотношения:
выполняются соотношения: 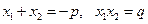 .
.
Т°.(обратная теореме Виета). Если для двух произвольных вещественных чисел 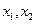 выполнены соотношения
выполнены соотношения 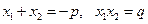 , то эти числа являются корнями приведенного квадратного уравнения
, то эти числа являются корнями приведенного квадратного уравнения 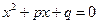 .
.
Т°. Квадратный трехчлен 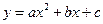 , для которого
, для которого 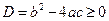 может быть разложен на линейные множители
может быть разложен на линейные множители 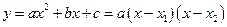 , где
, где 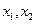 – корни квадратного уравнения
– корни квадратного уравнения 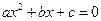 .
.
Графиком функции 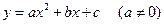 является парабола ветвями вверх при
является парабола ветвями вверх при 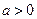 и, ветвями вниз при
и, ветвями вниз при 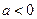 . Кроме того, парабола
. Кроме того, парабола 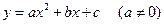 пересекает ось абсцисс в двух точках, если
пересекает ось абсцисс в двух точках, если 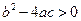 ,касается оси абсцисс не пересекая ее, если
,касается оси абсцисс не пересекая ее, если 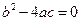 и не пересекает ось абсцисс если
и не пересекает ось абсцисс если 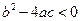 .
.
При построении графика функции 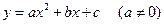 полезно помнить, что:
полезно помнить, что:
а) вертикальная прямая 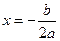 является осью симметрии параболы;
является осью симметрии параболы;
б) парабола пересекается с осью симметрии в точке, которая называется вершиной параболы и имеет координаты 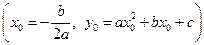 .
.
в) если 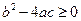 , то парабола пересекается с осью абсцисс в двух точках с координатами
, то парабола пересекается с осью абсцисс в двух точках с координатами 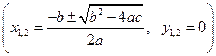 ; если
; если 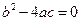 ,то эти точки совпадают между собой и совпадают с вершиной параболы; если
,то эти точки совпадают между собой и совпадают с вершиной параболы; если 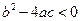 ,то парабола не имеет общих точек с осью абсцисс.
,то парабола не имеет общих точек с осью абсцисс.
г) парабола пересекает ось ординат в точке с координатами 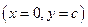 ; вместе с этой точкой на параболе лежит и точка
; вместе с этой точкой на параболе лежит и точка 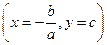 , симметричная ей относительно оси параболы.
, симметричная ей относительно оси параболы.
Задачи для решения:1*, 2*, …, 14*
1*. Найти все значения параметра а, при которых сумма корней уравнения 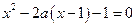 равна сумме квадратов этих корней.
равна сумме квадратов этих корней.
2*. Не решая уравнения 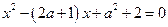 , установить значения параметра а, при которых один из корней уравнения в два раза больше другого.
, установить значения параметра а, при которых один из корней уравнения в два раза больше другого.
3*. Решить следующие уравнения, используя то, что они имеют общий корень:
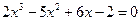 и
и 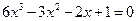 .
.
4*. Определить при каких значениях параметра а, один из корней уравнения
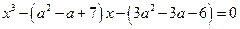 равен (–1). Найти остальные корни этого уравнения при установленных значениях параметра а.
равен (–1). Найти остальные корни этого уравнения при установленных значениях параметра а.
5*. Найти р и q если известно, что среди корней уравнения: x4 – 10x3 + 37x2 + px +q = 0 есть две пары равных между собой чисел.
6*. При каких m неравенство 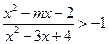 выполнено для любых х.
выполнено для любых х.
7*. При каких m корни уравнения: x2 + 2(m + 1)x + 9m – 5 = 0 отрицательны.
8*. При каких m корни уравнения: 4x2 – (3m + 1)x – m – 2 = 0 заключены в промежутке x Î[–1, 2].
9*. Найти коэффициенты уравнения x2 + px + q = 0 при условии, что разность его корней равна 5, а разность их кубов равна 35.
10*. При каком значении а оба корня уравнения
х2 – (а + 1)х + а + 4 = 0 будут положительны.
11*. При каких значениях m неравенство 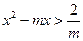 выполняется для любых значений х.
выполняется для любых значений х.
12*. При каких n корни уравнения: (n – 2)x2 – 2nx + n + 3 = 0 находятся на промежутке x Î[1, 4].
13*. При каких m неравенство 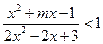 выполняется для любых значений х.
выполняется для любых значений х.
14*. При каких р система неравенств выполняется для любых х:
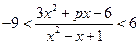 .
.
 2014-02-24
2014-02-24 1379
1379








