Формулы сокращенного умножения. Метод интервалов решения дробно-рациональных (и не только!) неравенств.
1.
ЭЛЕМЕНТЫ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
Формулы сокращенного умножения для запоминания:
1.  , 2.
, 2.  ,
,
3.  , 4.
, 4. 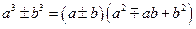 ,
,
5. 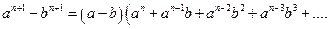
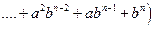 ,
,
6. 
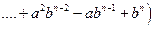 , n – четное.
, n – четное.
7. 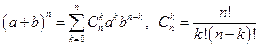 (Бином Ньютона).
(Бином Ньютона).
Одним из действенных методов решения рациональных (и не только) неравенств является, так называемый, метод интервалов.
Чтобы установить знак дроби с помощью этого метода следует:
1) Числитель и знаменатель дроби разложить на простейшие множители, корни которых легко найти;
2) На числовой оси отметить точки, в которых числитель или знаменатель дроби равен нулю;
3) Точки, в которых знаменатель обращается в ноль, исключить из рассмотрения;
После проделанного, числовая ось разобьется на интервалы, на каждом из которых знак дроби не изменяется. Установить знак дроби на каждом из таких интервалов можно непосредственной подстановкой произвольной точки интервала и вычислением знака дроби в этой точке.
Задачи для решения:1*, 2*, …, 12*, 13*
Применяя метод интервалов решить следующие неравенства:
1*.  , 2*.
, 2*.  ,
,
3*.  , 4*.
, 4*. 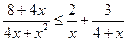 ,
,
5*. 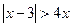 , 6*.
, 6*. 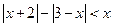 ,
,
7*.  , 8*.
, 8*. 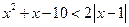 , 9*.
, 9*.  , 10*.
, 10*. 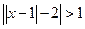 , 11*.
, 11*. 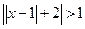 . 12*.
. 12*. 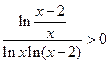 . 13*.
. 13*. 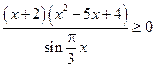 .
.
 2014-02-24
2014-02-24 779
779








