Процесс, протекающий при постоянной температуре, называется изотермическим.
| 1. Условие процесса 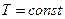 . Из уравнения состояния . Из уравнения состояния 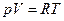 следует, что уравнение процесса следует, что уравнение процесса
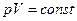 (12)
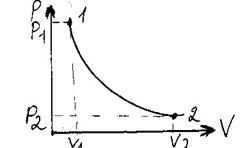
2.. В координатах (12)
2.. В координатах 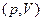 изотермический процесс изображается гиперболой: 1-2 – изотерма расширения, тепло подводится; 2-1 – изотерма сжатия, тепло отводится. изотермический процесс изображается гиперболой: 1-2 – изотерма расширения, тепло подводится; 2-1 – изотерма сжатия, тепло отводится.
|
| Рис.3. |
3. Для определения соотношения между параметрами воспользуемся уравнением (12)
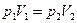 или
или 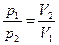 (13)
(13)
Изменение давления в изотермическом процессе обратно пропорционально изменению объема.
4. Изменение внутренней энергии для изотермического процесса равно нулю 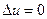 , так как температура не меняется. Работа, совершенная газом, определяется по формуле
, так как температура не меняется. Работа, совершенная газом, определяется по формуле
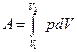 (14)
(14)
Выразим 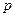 из уравнения состояния
из уравнения состояния
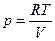 (15)
(15)
Подставив (15) в (14), получим
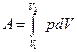 =
=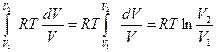 .
.
Учитывая, что 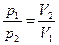 , работа равна
, работа равна
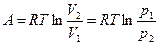 . (16)
. (16)
Запишем первое начало термодинамики
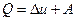 ,
,
но 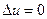 и
и 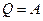 .
.
В изотермическом процессе все тепло подводимое к газу идет на совершение работы против внешних сил.
 2014-02-09
2014-02-09 555
555







