До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный – постоянный объем; изобарный – постоянное давление; изотермический – постоянная температура; адиабатный – при отсутствии теплообмена между рабочим телом и внешней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки.
Условились всякий процесс идеального газа, в котором теплоемкость является постоянной величиной, называть политропным процессом.
Из определения политропного процесса следует, что основные термодинамические процессы – изохорный, изобарный, изотермический и адиабатный, если они протекают при постоянной теплоемкости, являются частными случаями политропного процесса.
Теплоемкость политропного процесса 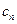 может принимать самые разнообразные положительные и отрицательные значения от
может принимать самые разнообразные положительные и отрицательные значения от 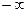 до
до 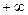 . Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости процесса
. Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости процесса 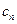 на разность температур.
на разность температур.
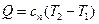 ,
,
или
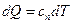
1. Уравнение политропического процесса выводится на основании первого закона термодинамики:
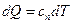 =
= 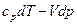
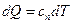 =
= 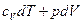 .
.
Преобразуем эти выражения
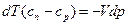
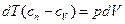 .
.
Разделим первое на второе
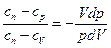 (1)
(1)
Введем обозначение
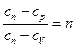 (2)
(2)
Тогда уравнение (1) примет вид
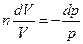 или
или 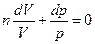 (3)
(3)
Выражение (3) является дифференциалом выражения 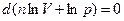 . Тогда
. Тогда
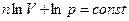 . (4)
. (4)
После потенцирования выражения (4) получим
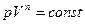 . (5)
. (5)
Уравнение (5) является уравнением политропического процесса, 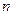 - показатель политропы.
- показатель политропы.
Теплоемкость политропного процесса определяется из формулы (2)
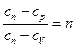
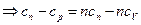
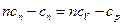 , так как
, так как 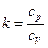 . Теперь
. Теперь
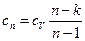 (6)
(6)
Из уравнений (6) и (2) можно получить значения теплоемкостей термодинамических процессов и показатели политропы. Все они занесены в таблицу.
| № | Процесс | 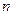 | 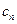 | Уравнение состояния. |
| 1. 2. 3. 4. | Изохорический Изобарический Изотермический Адиабатический | 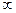 0 1 0 1 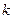 | 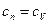 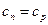 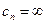 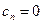 | 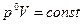 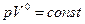 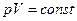 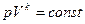 |
2. Поскольку уравнение политропы отличается от уравнения адиабаты только величиной показателя 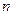 , то все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу.
, то все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу.
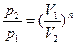 ,
, 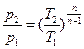 ,
, 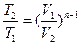 .
.
3. Изменение внутренней энергии газа и теплота в политропном процессе определяется по формулам
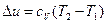 ,
,
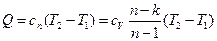 .
.
Уравнение работы изменения объема, совершаемой телом при политропном процессе имеет аналогичный вид с уравнением работы в адиабатном процессе
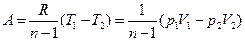 ,
,
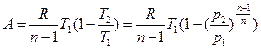 .
.
Значение 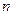 в любом политропном процессе может быть определено по параметрам двух состояний процесса.
в любом политропном процессе может быть определено по параметрам двух состояний процесса.
 | 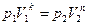 или или 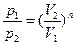 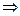 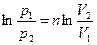 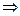 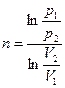 . . |
| Рис.2. |
Изображая политропный процесс в логарифмических координатах можно очень просто определить 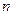 (рис.2).
(рис.2).
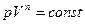 ,
,
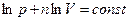 - это уравнение прямой в координатах
- это уравнение прямой в координатах 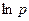 и
и 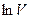 , а показатель политропы
, а показатель политропы 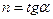 - тангенс угла наклона к оси абсцисс.
- тангенс угла наклона к оси абсцисс.
Все реальные процессы, протекающие в тепловых машинах, можно аппроксимировать политропными процессами с соответствующими показателями политропы, которые могут быть найдены по экспериментальным данным (по замерам давлений и удельных объемов в начальном и конечном состояниях газа).
4. Особенности распределения энергии в различных политропных процессах.
Рассмотрим расположение политропных процессов на 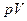 - диаграмме.(см. рис. 3),
- диаграмме.(см. рис. 3),
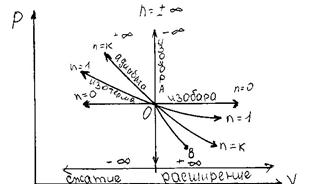 | выходящие из одной и той же точки, в зависимости от величины показателя. |
| Рис.3. |
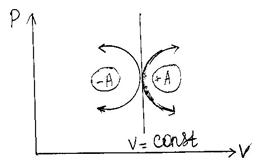 | . В процессах расположенных справа от изохоры газ совершает работу (+А), а расположенных слева – внешние силы совершают работу над газом (-А) (см. рис. 4) |
| Рис. 4. |
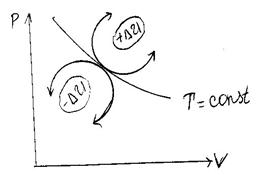 | Процессы, расположенные выше изотермы, протекают с увеличением внутренней энергии, а процессы расположенные ниже изотермы – с уменьшением внутренней энергии (см. рис. 5.) |
| Рис. 5. |
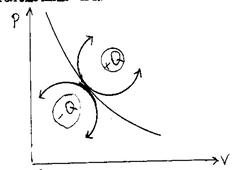 | Процессы, расположенные выше адиабаты, протекают с подводом тепла, а расположенные ниже – с отводом тепла. (см. рис. 6). |
| Рис. 6. |
Лекция 15
Второе начало термодинамики.
Сущность второго начала термодинамики.
 2014-02-09
2014-02-09 4769
4769
