Безынерционное (пропорциональное, усилительное) звено

Это звено, для которого в любой момент времени выходная величина пропорциональна входной.

Его уравнение: y(t) = k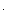u(t).

Передаточная функция: W(p) = k.

Переходная характеристика: h(t) = k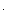1(t),(рис.33а).

а)

б)

в)

г)

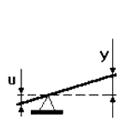
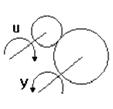
Рис. 33 Пропорциональное звено: а) переходная характеристика; б) рычаг; в) зубчатая безлюфтовая передача; г) потенциометр

В ответ на единичное ступенчатое воздействие сигнал на выходе мгновенно достигает величины в k раз большей, чем на входе и сохраняет это значение (рис.33). При k = 1 звено никак себя не проявляет, а при k = - 1 - инвертирует входной сигнал.

Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее j вместо p, получим АФЧХ W(j). Затем надо выразить из нее ВЧХ P() и МЧХ (Q(). После этого преобразуют АФЧХ в показательную форму и получают АЧХ A() и ФЧХ 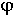(ω), а затем определяют выражение ЛАЧХ L(ω) = 20 lgA () (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс).

АФЧХ: W(j) = k.

ВЧХ: P() = k.

МЧХ: Q() = 0.

АЧХ: A() = k.

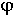ФЧХ: () = 0.

ЛАЧХ: L() = 20 lgk.

Некоторые ЧХ показаны на рис.34. Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе.

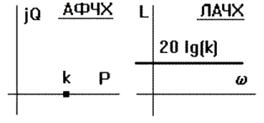
Рис. 34 Частотные характеристики пропорционального звена

Любое реальное звено обладает инерционностью, но с определенной точностью некоторые реальные звенья могут рассматриваться как безынерционные, например, жесткий механический рычаг, редуктор, потенциометр, электронный усилитель и т.п.