Его уравнение 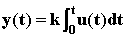 , или
, или 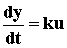 , или py = ku.
, или py = ku.
Передаточная функция: W(p) = k/p.
Переходная характеристика: 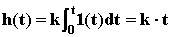 (рис.35).
(рис.35).
 а)
а)
|  б)
б)
|  в)
в)
|
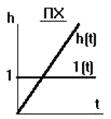
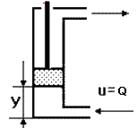
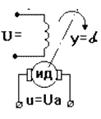
Рис. 35 Интегрирующее звено: а) переходная характеристика; б) гидравлический двигатель; в) электродвигатель постоянного тока
При k = 1 звено представляет собой “чистый” интегратор W(p) = 1/p. Интегрирующее звено неограниченно "накапливает" входное воздействие.
Рассмотрим частный случай, когда k = 1, то есть
W(p) = 1/p.
АФЧХ: W (j ) =
) = 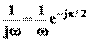 .
.
ВЧХ: P ( ) = 0.
) = 0.
МЧХ: Q ( ) = - 1/
) = - 1/ .
.
АЧХ: A ( ) = 1/
) = 1/ .
.
ФЧХ: 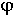 (
( ) = -
) = -  /2.
/2.
ЛАЧХ: L ( ) = 20 lg (1/
) = 20 lg (1/ ) = - 20 lg (
) = - 20 lg ( ).
).
ЧХ показаны на рис.36.
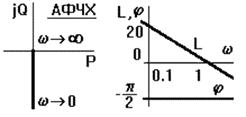
Рис. 36 ЧХ интегрирующего звена
Все частоты звено пропускает с запаздыванием по фазе на 90о. Амплитуда выходного сигнала увеличивается при уменьшении частоты, и уменьшается до нуля при росте частоты (звено "заваливает" высокие частоты). ЛАЧХ представляет собой прямую, проходящую через точку L ( ) = 0 при
) = 0 при  = 1. При увеличении частоты на декаду ордината уменьшается на 20 lg 10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду).
= 1. При увеличении частоты на декаду ордината уменьшается на 20 lg 10 = 20дб, то есть наклон ЛАЧХ равен - 20 дб/дек (децибел на декаду).
Примеры интегрирующих звеньев: электродвигатель, поршневой гидравлический двигатель, емкость и т.п. Введение его в САУ превращает систему в астатическую, то есть ликвидирует статическую ошибку.
Инерционное звено первого порядка (апериодическое)
Уравнение динамики: 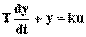 , или Tpy + y = ku.
, или Tpy + y = ku.
Передаточная функция: W(p) = 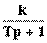 .
.
Переходная характеристика может быть получена с помощью формулы Хевисайда:
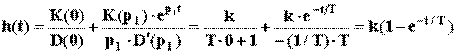 ,
,
где p1 = - 1/T - корень уравнения D(p) = Tp + 1 = 0; D’(p1) = T.
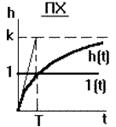
Переходная характеристика имеет вид экспоненты (рис.37), по которой можно определить передаточный коэффициент k, равный установившемуся значению h(t), и постоянную времени Т по времени t, соответствующему точке пересечения касательной к кривой в начале координат с ее асимптотой. При достаточно больших Т звено на начальном участке может рассматриваться как интегрирующее, при малых Т звено приближенно можно рассматривать как безынерционное.
 а)
а)
|  б)
б)
|  в)
в)
|  г)
г)
|
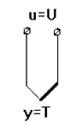
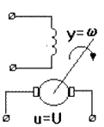
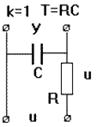
Рис. 37.Апериодическое звено: а) переходная характеристика, б) термопара, в)электродвигатель, г) четырехполюсник
При k = 1 получаем следующие выражения ЧХ:
W(p) = 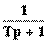 ;
;
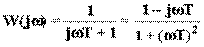 ;
;
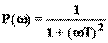 ;
;
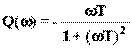 ;
;
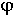 (
( ) =
) = 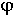 1 -
1 - 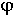 2 = - arctg(
2 = - arctg( T);
T);
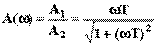 ;
;
L( ) = 20lg(A(
) = 20lg(A( )) = - 10lg(1 + (
)) = - 10lg(1 + ( T)2).
T)2).
Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ; 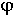 1 и
1 и 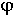 2 - аргументы числителя и знаменателя. ЛФЧХ:
2 - аргументы числителя и знаменателя. ЛФЧХ:
ЧХ показаны на рис.38. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при  <
<  1 = 1/ T можно пренебречь (
1 = 1/ T можно пренебречь ( T)2 выражении для L (
T)2 выражении для L ( ), то есть L (
), то есть L ( )
) 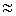 - 10 lg1 = 0.. При
- 10 lg1 = 0.. При 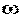 >
> 1 пренебрегают единицей в выражении в скобках, то есть L(
1 пренебрегают единицей в выражении в скобках, то есть L(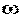 )
) 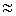 - 20 lg(
- 20 lg( 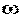 T). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота
T). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота 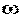 1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при
1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при  =
=  1.
1.
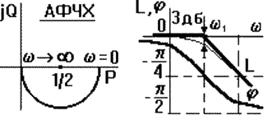
Рис. 38.ЧХ апериодического звена
ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к -  /2 при возрастании
/2 при возрастании  до бесконечности. Перегиб в точке
до бесконечности. Перегиб в точке  =
=  1 при
1 при 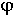 (
( ) = -
) = -  /4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
/4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
Примеры апериодического звена: термопара, электродвигатель, четырехполюсник из сопротивления и емкости или сопротивления и индуктивности.
 2014-02-24
2014-02-24 901
901








