Тема 6 Линейная корреляция
Задания для самостоятельной работы.
1. Привести свои примеры возможных корреляций.
2. Составить по представленному в главе образцу диаграмму корреляционной зависимости между показателями веса и роста в группе студентов (например, в Вашей группе) или школьников. Объем выборки должен быть не менее 15 человек. К диаграмме приложить таблицу значений.
3. Составить диаграмму корреляционной зависимости показателей субтестов «осведомленность» и «скрытые фигуры» (Таблица I Приложения) для первых 12 человек.
Коэффициент корреляции Пирсона называется также коэффициентом линейной корреляции или произведением моментов Пирсона. Он позволяет определить силу связи между двумя признаками, измеренными в метрических шкалах.
Его формула выглядит следующим образом:
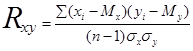

У разных авторов эта формула может выглядеть по-разному. В данном пособии формула приводится в том виде, как она дана в кн. Наследов А.Д., Тарасов С.Г. «Применение математических методов в психологии».
Последовательность расчетов можно продемонстрировать на следующем примере. Итак, необходимо:
1. Вычислить значение корреляции между показателями роста в сантиметрах и веса в килограммах у представителей группы студентов.
2. Поставить вопрос о достоверности этого коэффициента. Для решения второй задачи необходимо предварительно сформулировать нулевую и альтернативную гипотезы:
Н0: корреляция между показателями роста и веса значимо не отличается от нуля (является случайной).
Н1: корреляция между показателями роста и веса значимо отличается от нуля (является неслучайной).
3. Данные заносятся в таблицу, при этом желательно, чтобы один из столбцов значений признака (показатели роста или веса) был упорядочен. 
| № | X (рост) | Y (вес) | xi-Мх | (xi-Мх)2 | yi-Му | (yi-Му)2 | (xi-Mx)*(yi-My) |
| -7,6 | 57,76 | -11,3 | 127,69 | 85,88 | |||
| -6,6 | 43,56 | -9,3 | 86,49 | 61,38 | |||
| 5,4 | 29,16 | 6,7 | 44,89 | 36,18 | |||
| -6,6 | 43,56 | -1,3 | 1,69 | 8,58 | |||
| 10,4 | 108,16 | 12,7 | 161,29 | 132,08 | |||
| -3,6 | 12,96 | -8,3 | 68,89 | 29,88 | |||
| -2,6 | 6,76 | 0,7 | 0,49 | -1,82 | |||
| -0,6 | 0,36 | 9,7 | 94,09 | -5,82 | |||
| 8,4 | 70,56 | 4,7 | 22,09 | 39,48 | |||
| 3,4 | 11,56 | -4,3 | 18,49 | -14,62 | |||
| n=10 | Мх=166,6 | Мy=58,3 | Σ(xi-Mx)2=384,4 | Σ(yi-My)2=626,1 | Σ(xi-Mx)*(yi-My)=371,2 |
σх =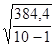 ≈ 6,53 σу =
≈ 6,53 σу =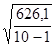 ≈ 8,34
≈ 8,34
Rxy = 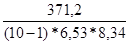 ≈ 0,758
≈ 0,758
 2014-02-24
2014-02-24 755
755








