Приведем порядок (алгоритм) решения любой задачи (проблемы)

В реальных условиях присутствуют все три механизма передачи, но вклад каждого в каждом конкретном случае может быть разным. Пример: охлаждение слитка или отливки на воздухе осуществляется так называемым сложным теплообменом

S - коэффициент излучения, Вт/м2к4.

Q_S=Q_Т+Q_К+Q_Л ,

где Q_Т, Q_К, Q_Л – тепловые потоки теплопроводностью, конвекцией и излучением. При высоких температурах преобладает излучение, тогда Q_S» Q_Л.

Для простоты изложения будем все три механизма изучать по отдельности.

1. ТЕПЛОПРОВОДНОСТЬ

1.1 Температурное поле. Температурное поле – это совокупность значений температур в данный момент времени t для всех точек изучаемого пространства. Математическая запись: t=f(x,y,z,t). (Бывают поля скоростей, давлений, напряжений, концентраций, электрические, магнитные, электромагнитные, гравитационные, биополя и т.д.) Изложенные ниже основы расчета температурных полей могут быть применены к расчету других полей. t=f₃(x)®одномерное стационарное температурное поле. Возможны случаи, когда t=f₂(x,y) – двухмерное стационарное, а если t=f₄(x,t) – одномерное нестационарное, а при t=f₅(t) – нольмерное нестационпрное, это нагрев термически тонкого тела.

Определение 1. Изотермическая поверхность – это геометрическое место точек, имеющих одинаковую температуру.

Свойства изотерм: изотермы не должны пересекаться, это функция однозначная, т.к. одна и та же точка не должна иметь две разные температуры

1.2. Градиент температур.

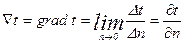, град/м. Градиент температур - это предел отношения изменения температуры к расстоянию между изотермами по нормали n.

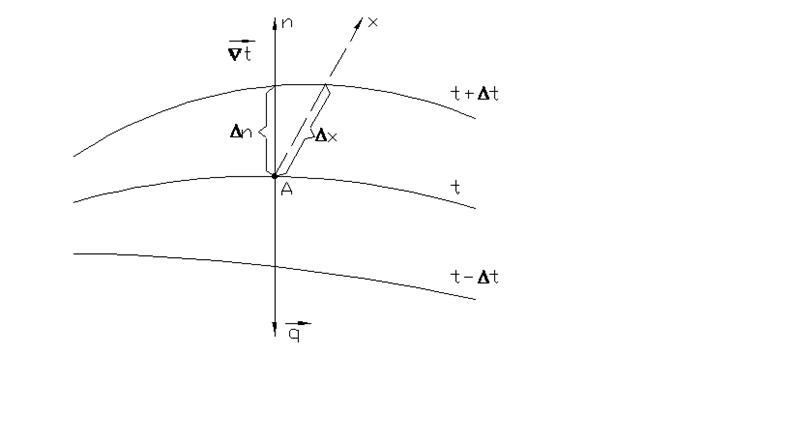
Рис. 1.1 Изотермы и градиент температур

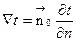(1.1)

Ñt- это вектор, направленный в сторону возрастания температур (или другой величины).

Второе определение. Температурный градиент представляет собой максимальное изменение температуры на единицу длины в направлении нормали n к изотерме. 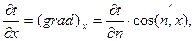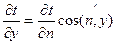и т.д. Пример: слиток .

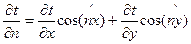1.3. Основной закон теплопроводности. Постулат Фурье о пропорциональности теплового потока градиенту: q~grad t после многочисленных опытных проверок превратился в Закон, названный его именем: 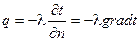, Вт/м². (1.2)

Закон Фурье (2) называют основным законом теплопроводности.

Для одномерного стационарного поля температур закон Фурье упрощается до вида:

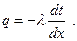(1.3)

Так как тепловой поток является вектором, то его можно записать в проекциях на оси x,y,z.

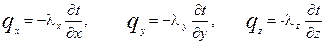
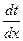Знак " –" поставлен из тех соображений, что тепловой поток, будучи вектором, направлен в сторону убывания температуры, т.е. в противоположную сторону чем градиент температур.

Полное количество теплоты найдем путем интегрирования по поверхности и времени следующего выражения: ,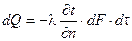

Тогда 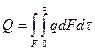, (1.4)

l–это коэффициент пропорциональности в законе Фурье, показывает какое количество тепла передается в 1^цу времени при градиенте t=1⁰/м, [l] =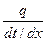= Вт/м×К. Коэффициент теплопроводности l–характеризует способность тела проводить теплоту. l - это физический параметр, зависящий от природы тела, температуры, давления (для газов) и от направления (для анизотропных тел), например: древесина, материалы в рулонах и т.д. Существует тесная аналогия между протеканием электричества и теплоты. Поэтому хорошие проводники электричества (золото, серебро, медь) одновременно являются хорошими проводниками теплоты. Коэффициенты теплопроводности таких тел Вт/мК.

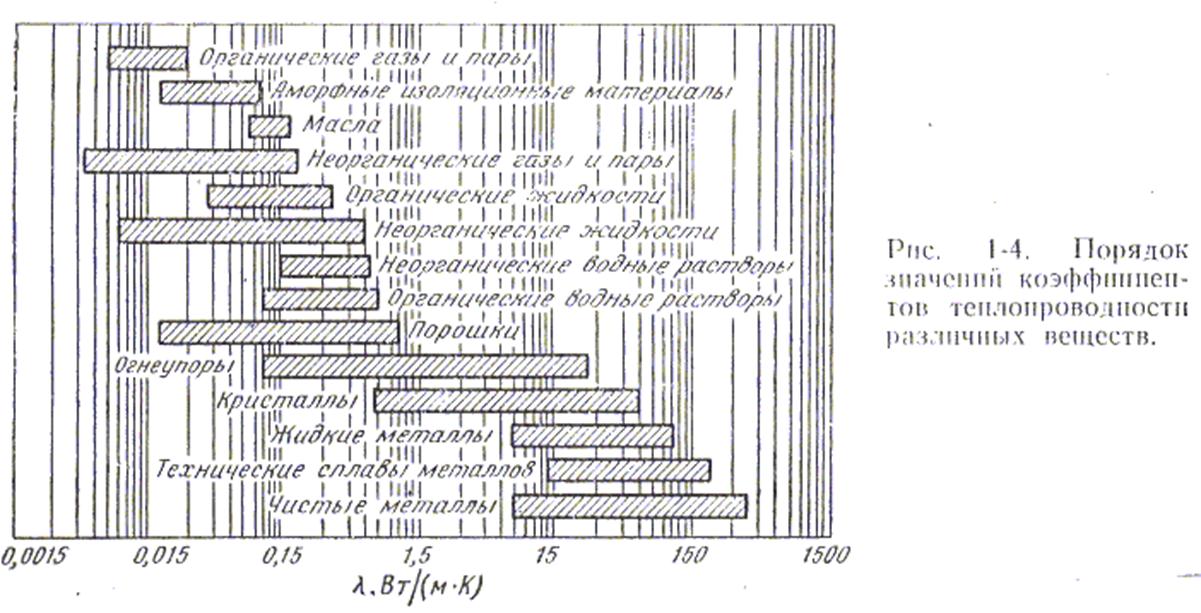Рис. 1.2 Порядок значений коэффициентов теплопроводности различных веществ

1.4. Дифференциальное уравнение теплопроводности

При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. Для сложных физических явлений, когда исходные величины могут существенно меняться в пространстве и времени на помощь приходит метод математической физики. Сущность метода: ограничивается отрезок времени от t до t+dt и из всего пространства V выделяется элементарно малый объём тела dV.

Вывод уравнения основывается на законе сохранения энергии или I-м законе термодинамики, записанного для dV и dt. Получим уравнение в декартовой системе координат, тогда .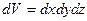

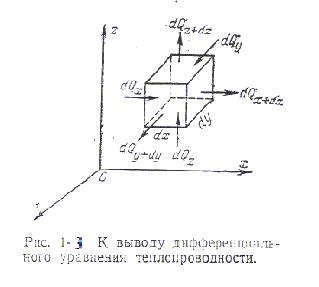
Полное количество теплоты, полученное телом 3

Q=cmΔT=cρVΔT или в дифференциальном виде dQ₁=cρdVdT где ΔT=T_конечн-T_нач=(Т+dT)-T=dT. С другой стороны, используя понятие удельного теплового потока вдоль оси Х

dQ=Dq×dF×dt, где ∆q=q_x-(q_x+dq_x)=-dq_х. Согласно закону сохранения энергии должно быть Q₁=Q₂ или тепловой баланс в дифференциальной форме: 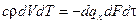. Учтя, что 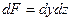, разделив уравнение на dV и dt и используя закон Фурье: 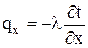и т.д., получим

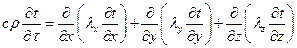(1.5)

или в более компактном виде

.

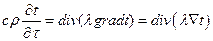Если внутри тела действуют источники (стоки) теплоты, то в правую часть уравнений добавляется величина q_V – объемная плотность внутренних тепловыделений.

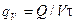, Вт/м³.

1.4.1. Анализ дифференциального уравнения теплопроводности

Оно устанавливает связь между временным (t) и пространственным 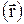изменением температуры в любой внутренней точке тела, в котором происходит процесс теплопроводности.

Для простоты анализа примем, что тело изотропное, когда его теплофизические свойства не зависят от направления. Пусть также коэффициент теплопроводности не зависит от температуры. Тогда 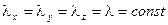и уравнение теплопроводности (4) упрощается

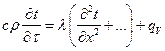. (1.6)

Существует более компактная форма записи дифференциального уравнения теплопроводности

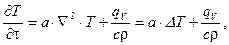(1.7)

где 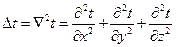– лапласиан, Набла в квадрате или оператор Лапласа в декартовой системе координат; 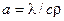- коэффициент температуропроводности, м²/с.

Запись оператора Лапласа в других системах координат:

а) цилиндрическая: 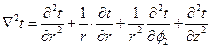, (1.8)

б) сферическая: 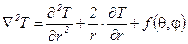, (1.9)

где j - азимутальный угол или угол долготы (меридианы), q - угол широты (параллели).

Для одномерного поля температур можно записать общее уравнение:

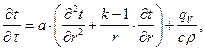(1.10)

где k – фактор геометрической формы равный 1 – для плоского тела, 2 – цилиндра и 3 для шара.

Рассмотрим физический смысл коэффициента температуропроводности а.

1) это физический параметр, зависящий от рода вещества и в основном от температуры;

2) существенен только для нестационарных процессов;

3) характеризует скорость изменения температуры, т.е. а – представляет меру теплоинерционных свойств. Это вытекает из уравнения (1.7), т.к. 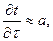то скорость изменения температуры будет тем больше, чем больше а. Т.е. выравнивание температур будет быстрее происходит в том теле, где температуропроводность больше.

Т.к. 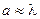, то можно составить такую "цепочку" неравенств:

а_{металлов}>а_{жидкости}>а_газов

Анализ 1) Пусть 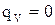. Получим уравнение Фурье: 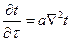(1.11)

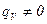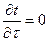
2) , 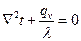уравнение Пуассона (1.12)

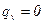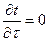
3) , 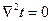уравнение Лапласа (1.13)

В уравнениях (12) и (13) температуропроводность отсутствует, т.е.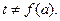

4) ;

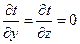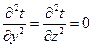
когда 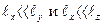, то получено одно мерное уравнение 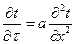. (1.14)

Нахождение решений этих уравнений в частных производных представляет собой основное содержание теории теплопроводности.

1.4.2. Краевые условия.

Уравнение (1.4) описывает процесс теплопроводности в самом общем виде, т.е. описывает целый класс явлений теплопроводности.

Пример: Пусть дано дифференциальное уравнение 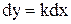, его решение: 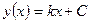, где С – постоянная интегрирования. Это набор прямых линий. Если уравнение 2-го порядка, то возникнут две постоянные и т.д. Для определенности решения нужно добавить краевые условия (КУ) или условия однозначности.

Определение.

КУ – это частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса. Следует различать условия однозначности:

1) геометрические –– должны быть заданы форма и размеры тела

2) физические l, с, r, q_v(x,t) и др.

3) начальные (временные) если 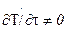, то задается начальное распределение температуры .

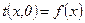Часто принимают .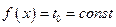

4) Граничные условия (ГУ) – характеризуют взаимодействие тела с окружающей средой.

Существует несколько способов задания граничных условий:

ГУ I pода - задано распределение температур на поверхности:

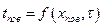, часто .

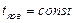ГУ II pода - задан тепловой поток на поверхности

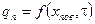; т.е. .

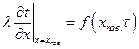Часто полагают . Например, первый период нагрева металла в нагревательных колодцах.

ГУ III pода - Заданы температура окружающей среды и закон теплообмена между средой и поверхностью тела. Чаще всего используется закон Ньютона-Рихмана:

q_пов=q_конв., т.е. ,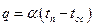

где a- коэффициент теплоотдачи Вт/м²К, характеризует интенсивность теплоотдачи между поверхностью тела и окружающей средой.

; .

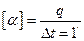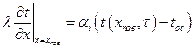Для высокотемпературных процессов должен учитываться нагрев тел излучением

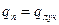или .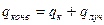

ГУ IV рода – когда заданы температуры и тепловые потоки в местах контакта двух разных тел:

.

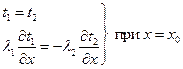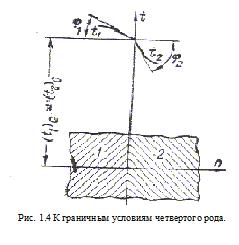
Дифференциальное уравнение совместно с условием однозначности дают полную математическую формулировку задачи теплопроводности, т.е. задачи нахождения температурного поля в твердом теле.

Эта задача может быть решена:

1) экспериментально; 2) теоретически.

1. Ставится ФПЗ (физическая постановка задачи). Дано – найти. Цель.

2. Проводится обзор работ, патентно-информационный поиск (ПИП). Наброски математической модели.

3. Ставится МПЗ (математическая постановка задачи). Проводится анализ МПЗ.

4. Выбор и обоснование метода решения. АВМ, ЭЦВМ, эксперимент – что есть в наличии.

5. Решение задачи.

6. Анализ полученного решения

7. Выводы и рекомендации.

1.5 Стационарная теплопроводность

1.5.1. Теплопроводность плоской однослойной стенки.

Рассмотрим наиболее простые случаи.

а) физическая постановка задачи. Пусть дана неограниченная плоская однослойная стенка толщиной d (Рис.1.5).

Рис. 1.5 Теплопроводность в плоской стенке

Пусть коэффициент теплопроводности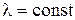. Известны температуры на левой поверхности t_п.1, а на правой – t_п.2, которые не изменяются со временем. Внутренние источники теплоты отсутствуют, т.е. q_V= 0. Температуры t вдоль осей OY и OZ=const. Тогда .

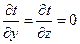Задача: Требуется найти распределение температур по сечению t(x) и тепловой поток q через стенку.

б) математическая постановка: для расчета процесса теплопроводности следует использовать уравнение (1.7) в декартовой системе координат заменим 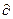на d, т.к. стенка плоская и температура зависит только от одной переменной х. Учтем, что температуры неизменны во времени, т.е.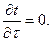

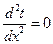; (1.15)

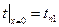; (1.16)

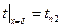(1.17)

Решение диференциального уравнения (1.15): 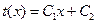; (1.18)

С помощью граничных условий (1.16) и (1.17) найдем постоянные 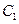и 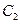. Полагая в уравнении (1.16) х=0, получим 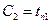, затем х=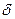в (1.17). Тогда .

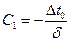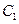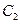Подставляя в (1.18) и , получим 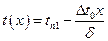, (1.19)

где ;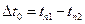

Анализ полученного решения.

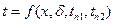. Температура согласно (19) меняется вдоль стенки по линейному закону.

Весьма удобно представить решение в безразмерном ви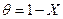де: , где 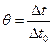, , 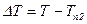т.е.отсчет ведем от наименьшей температуры.

2) Тепловой поток согласно закону Фурье: ,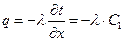

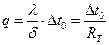, (1.20)

где 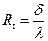м²К/Вт – термическое сопротивление плоской стенки.

3а) 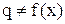другой вид решения (1.19)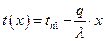

3б) Полное количество теплоты 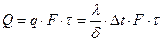, Дж.

4) Если учесть зависимость коэффициента теплопроводности, например, пусть 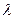изменяется по линейному закону 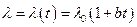, то где решение будет иметь вид

,

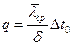где ,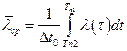

Распределение температур 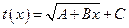– уже будет не прямая, а кривая линия.

1.5.2. Теплопроводность плоской многослойной стенки.

Дано: число слоев m, режим стационарный

Известны: t_n1 и t_n(нар) (Рис. 1.6)

Найти: q и t_{пов.внутр.}

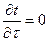, пользуемся случаем, что .

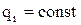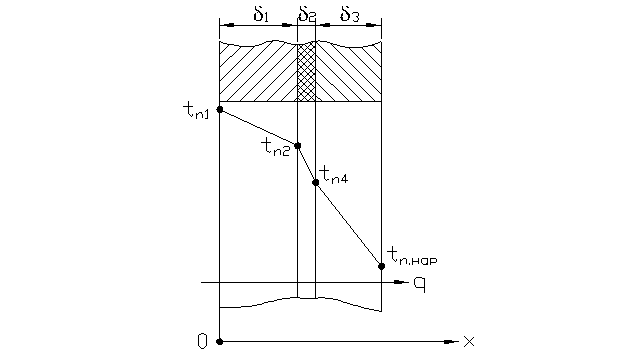
Рис. 1.6. Теплопроводность плоской многослойной стенки

Запишем тепловые потоки для каждой стенки согласно уравнению (1.20) 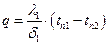, найдем разность температур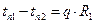

,

………………………………………………………….

, .

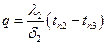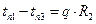
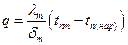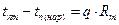Определив DT – (температурные напоры) и сложив левые и правые части полученных уравнений, получим .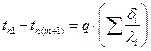

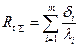– полное термическое сопротивление многослойной стенки равное сумме R_Т всех слоев. Тогда удельный тепловой поток через многослойную стенку

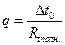(1.21)

Зная q, найдем температуры в местах контакта стенок t_ni: 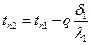и т.д. .

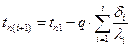1.5.3. Теплопередача через плоскую однослойную стенку

ОПРЕДЕЛЕНИЕ. Передача тепла от одной более горячей среды (жидкости или газа) к другой холодной, через разделяющую их одно или многослойную стенку любой формы называется теплопередачей.