Первый корень уравнения (4.9) вычисляем по соотношению (4.23) при 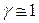 и
и 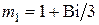 , а второй — по (4.24). Тогда отношение собственных чисел или коэффициентов термической массивности
, а второй — по (4.24). Тогда отношение собственных чисел или коэффициентов термической массивности
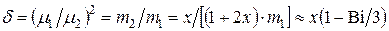 , (4.28)
, (4.28)
где 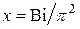 .
.
Разность квадратов корней 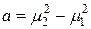
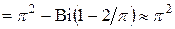 .
.
Первая амплитуда, входящая в уравнение (4.6) температуры поверхности
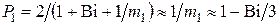 . (4.29)
. (4.29)
По аналогии вторая 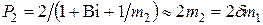 и
и
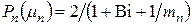 . (4.30)
. (4.30)
Амплитуда 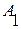 согласно уравнению (4.27) и с учетом того, что при малых аргументах
согласно уравнению (4.27) и с учетом того, что при малых аргументах 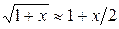 :
:
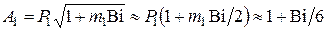 . (4.31)
. (4.31)
Амплитуда 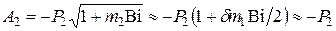 .
.
Для среднемассовой температуры:
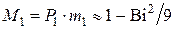 и
и 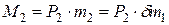 . (4.32)
. (4.32)
Для перепада температур по уравнению (4.11)
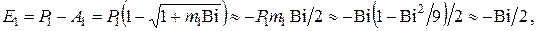 (4.33)
(4.33)
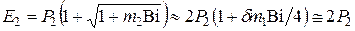 .
.
Для термических напряжений в центре пластины по (4.4)
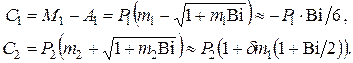 (4.34)
(4.34)
Для термонапряжений на поверхности
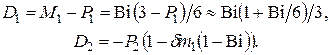 (4.35)
(4.35)
С целью проверки амплитуды 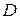 можно использовать равенство
можно использовать равенство 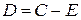 .
.
Выражения для расчета максимальных времен по уравнению (4.18) также упростятся.
Коэффициент поверхности 
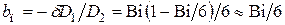 ,
,
для перепада температур 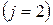
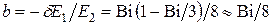 (4.36)
(4.36)
и центра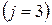
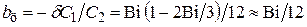 .
.
Анализ уравнений (4.18) и (4.36) позволяет сделать вывод о том, что максимум величин наступает в последовательности 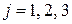 и с ростом числа Био эти времена уменьшаются.
и с ростом числа Био эти времена уменьшаются.
Для оценки различия максимальных времен составим их разности:
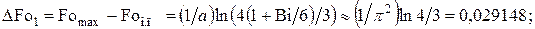
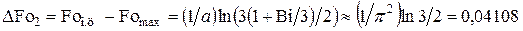 (4.37)
(4.37)
и 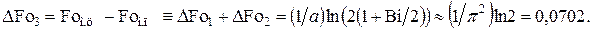
Из (4.37) следует, что с ростом числа Био различия максимальных времен увеличиваются, вплоть до 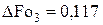 – см. уравнение (4.45).
– см. уравнение (4.45).
На практике технологов интересует вопрос — насколько термические напряжения на поверхности тела больше, чем в его середине. Обозначим их отношение 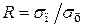 . Наиболее просто
. Наиболее просто 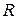 можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье
можно найти в стадии регулярного режима нагрева (РРН), который наступает при числах Фурье 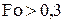 и когда вместо бесконечных сумм в уравнениях (4.3)…(4.11) можно ограничиться одним членом ряда. Тогда, деля уравнение (4.3) на (4.4) и учитывая упрощенные соотношения (4.34) и (4.35), получим
и когда вместо бесконечных сумм в уравнениях (4.3)…(4.11) можно ограничиться одним членом ряда. Тогда, деля уравнение (4.3) на (4.4) и учитывая упрощенные соотношения (4.34) и (4.35), получим
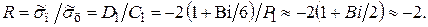 (4.38)
(4.38)
4.1.2. Асимптотика при больших числах Био.
Теперь корни 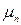 находим по уравнению (4.25). Тогда отношение
находим по уравнению (4.25). Тогда отношение
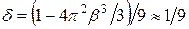 . (4.39)
. (4.39)
Разность квадратов корней
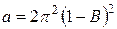 , (4.40)
, (4.40)
где 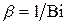 ;
; 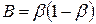 .
.
Амплитуды:
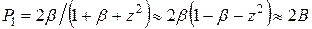 ;
; 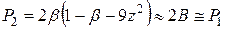 ,
,
где 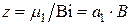 ;
; 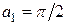 .
.
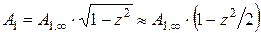 ;
; 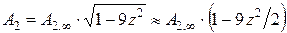 ,
,
где 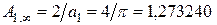 и
и 
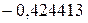 — амплитуды при
— амплитуды при 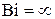 .
.
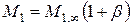 ;
;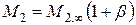 где
где 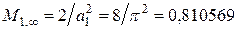 ;
; 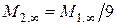 .
.
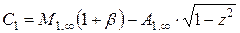 ;
; 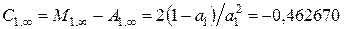 ;
;
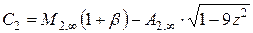 ;
; 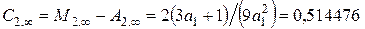 .
.
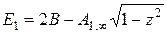 ;
; 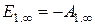 ;
; 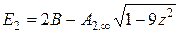 ;
; 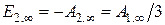 .
.
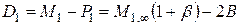 ;
; 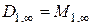 ;
; 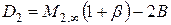 ;
; 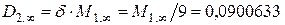 .
.
Теперь коэффициенты для расчета максимальных времен примут вид:
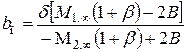 ; (4.41)
; (4.41)
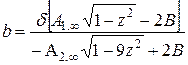 ; (4.42)
; (4.42)
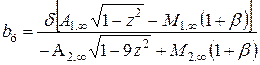 ; (4.43)
; (4.43)
В предельном случае при 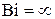 :
:
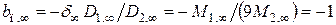 ;
;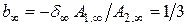 ;
;
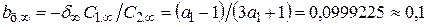 . (4.44)
. (4.44)
Так как 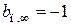 лишено физического смысла, следует взять
лишено физического смысла, следует взять 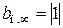 .
.
Тогда наименьшие максимальные времена согласно (4.18) при 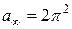 будут:
будут:
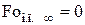 ,
, 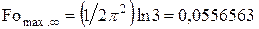 ,
,
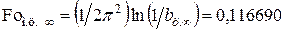 . (4.45)
. (4.45)
Подставляя (4.45) в уравнение (4.4), получим максимально возможное термическое напряжение в центре пластины
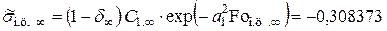 . (4.46)
. (4.46)
Термонапряжение на поверхности при времени 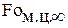
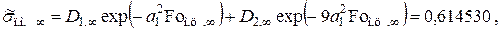
перепад температур
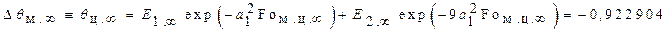
и отношение напряжений в этот момент времени
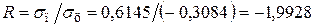 .
.
Последнее несколько больше, чем отношение 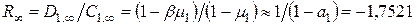 , которое получено для стадии РРН с учетом первого члена ряда.
, которое получено для стадии РРН с учетом первого члена ряда.
Следует отметить, что если приближенно считать 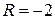 , то из уравнения (4.10) будем иметь
, то из уравнения (4.10) будем иметь
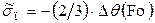 (4.47)
(4.47)
и это соотношение полностью совпадает с формулой Н.Ю. Тайца [28]
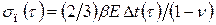 . (4.48)
. (4.48)
Из анализа уравнения (4.41) вытекает, что коэффициент 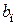 меняет знак по причине изменения знака амплитуды
меняет знак по причине изменения знака амплитуды 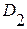 , изменяющейся от
, изменяющейся от 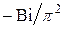 при малых числах Био до
при малых числах Био до 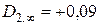 . Из условия равенства нулю
. Из условия равенства нулю 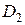 можно получить граничное число
можно получить граничное число 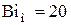 выше которого имеем случаи нагрева термически «массивного» тела. Таким образом, при числах
выше которого имеем случаи нагрева термически «массивного» тела. Таким образом, при числах 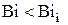 для определения времени
для определения времени 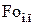 можно применять формулу (4.12) в которой
можно применять формулу (4.12) в которой 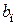 определяется по уравнению (4.41), а при
определяется по уравнению (4.41), а при 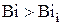 коэффициент
коэффициент 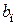 становится отрицательным и нельзя пользоваться формулой (4.12).
становится отрицательным и нельзя пользоваться формулой (4.12).
Возникшую ситуацию можно объяснить следующим образом. Формулы (4.12)…(4.22) получены с учетом всего двух членов ряда. С ростом числа Био максимальное время 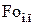 уменьшается, вплоть до 0 при
уменьшается, вплоть до 0 при 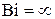 .
.
При очень малых числах Фурье 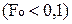 расчёт температур по уравнениям (4.3)…(4.11) затруднителен из-за необходимости учета большого количества членов ряда, ввиду его плохой сходимости. В этом случае для расчёта поверхностной и среднемассовой температур можно использовать формулы, полученные методом операционного исчисления в работе [10] (см. уравнения (3.25)…(3.27))
расчёт температур по уравнениям (4.3)…(4.11) затруднителен из-за необходимости учета большого количества членов ряда, ввиду его плохой сходимости. В этом случае для расчёта поверхностной и среднемассовой температур можно использовать формулы, полученные методом операционного исчисления в работе [10] (см. уравнения (3.25)…(3.27))
С учетом сказанного уравнение (4.3) для расчета термических напряжений на поверхности примет вид
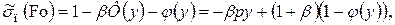 (4.49)
(4.49)
где 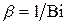 .
.
Вместо уравнения (4.6) будет (3.25), а вместо (4.8) — (3.26). Температуру в центре тела на начальной стадии нагрева (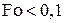 ) приближенно можно принять
) приближенно можно принять 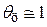 .
.
Дифференцируя уравнение (4.49) по времени и приравнивая производную нулю, получим при малых (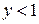 )
)
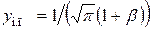 ,
,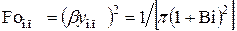 (4.50)
(4.50)
и больших аргументах (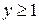 )
)
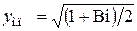 ,
, 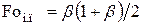 . (4.51)
. (4.51)
Таким образом, при больших числах Био (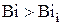 ) расчет времени
) расчет времени 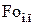 вместо (4.12) следует производить по уравнению (4.50) или (4.51).
вместо (4.12) следует производить по уравнению (4.50) или (4.51).
Расчет 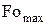 по (4.13) с учетом (4.42) даст
по (4.13) с учетом (4.42) даст
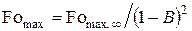 . (4.52)
. (4.52)
Иногда требуется определить расположение координаты 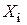 нейтрального слоя в котором термические напряжения меняют знак с
нейтрального слоя в котором термические напряжения меняют знак с 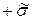 на
на 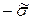 , т.е. в этой точке равны нулю. Наиболее просто это можно сделать в стадии РРН. Тогда согласно уравнению (4.2)
, т.е. в этой точке равны нулю. Наиболее просто это можно сделать в стадии РРН. Тогда согласно уравнению (4.2) 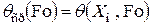 или
или 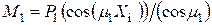 .
.
Разрешая последнее выражение относительно 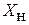 , получим
, получим
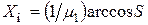 , (4.53)
, (4.53)
где 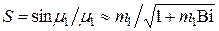 .
.
При малых числах Био 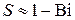 . Тогда с учетом тригонометрического тождества
. Тогда с учетом тригонометрического тождества 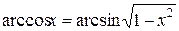 и разложения в ряд
и разложения в ряд 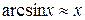 , будем иметь
, будем иметь
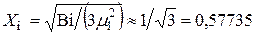 . (4.54)
. (4.54)
При больших числах Био
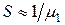 и
и 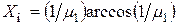 . (4.55)
. (4.55)
В предельном случае при 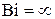 ,
, 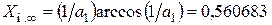 . Таким образом, поскольку
. Таким образом, поскольку 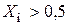 нейтральные слои расположены несколько ближе к поверхности, а само
нейтральные слои расположены несколько ближе к поверхности, а само 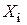 колеблется в узких пределах — от 0,56 до 0,58.
колеблется в узких пределах — от 0,56 до 0,58.
Следует отметить, что при нагреве абсолютные, т.е. размерные термические напряжения 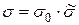 поменяют знаки за счет отрицательности
поменяют знаки за счет отрицательности 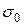 из-за
из-за 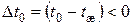 .
.
В заключение укажем, что все полученные решения описывают как процесс конвективного нагрева плоских тел, так и их охлаждение.
 2014-02-24
2014-02-24 770
770








