Таблица 2.4
Рис.2.22
Рис.2.18
Рис.2.17
Рис. 2.15
Для испытаний на растяжение применяют разрывные машины, позволяющие в процессе испытания записать диаграмму в координатах “нагрузка – абсолютное удлинение”. Характер диаграммы растяжения зависит от свойств испытуемого материала и от скорости деформирования. Типичный вид такой диаграммы для малоуглеродистой стали при статическом приложении нагрузки изображен на рис. 2.16.
Рассмотрим характерные участки и точки этой диаграммы, а также соответствующие им стадии деформирования образца:
ОА – справедлив закон Гука;
АВ – появились остаточные (пластические) деформации;
ВС – пластические деформации растут;
СД – площадка текучести (рост деформации происходит при постоянной нагрузке);
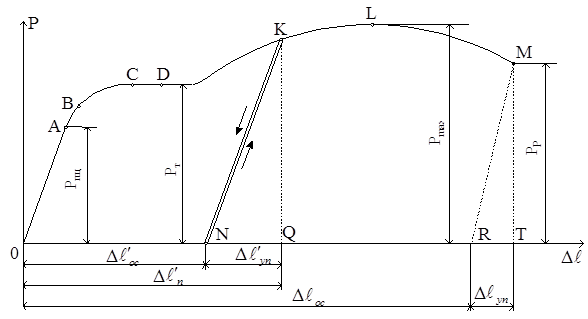
Рис.2.16
ДК – участок упрочнения (материал вновь приобретает способность увеличивать сопротивление дальнейшей деформации и воспринимает возрастающее до некоторого предела усилие);
Точка K – испытание остановили и произвели разгрузку образца;
KN – линия разгрузки;
NKL – линия повторного нагружения образца (KL – участок упрочнения);
LM – участок падения нагрузки, в этот момент на образце появляется так называемая шейка - местное сужение;
Точка M – разрыв образца;
После разрыва образец имеет вид, примерно показанный на рис.2.17. Обломки можно сложить и измерить длину после испытания ℓ1, а также диаметр шейки d1.
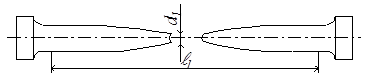
В результате обработки диаграммы растяжения и измерений образца получаем ряд механических характеристик, которые можно разделить на две группы – характеристики прочности и характеристики пластичности.
Характеристики прочности
Предел пропорциональности:
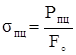 . (2.21)
. (2.21)
Наибольшее напряжение, до которого справедлив закон Гука.
Предел текучести:
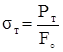 . (2.22)
. (2.22)
Наименьшее напряжение, при котором деформация образца происходит при постоянном растягивающем усилии.
Предел прочности (временное сопротивление):
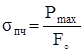 . (2.23)
. (2.23)
Наибольшее напряжение, отмеченное в процессе испытания.
Напряжение в момент разрыва:
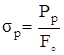 . (2.24)
. (2.24)
Определяемое таким образом напряжение при разрыве весьма условно и не может быть использовано в качестве характеристики механических свойств стали. Условность состоит в том, что получено оно делением силы в момент разрыва на первоначальную площадь поперечного сечения образца, а не на действительную его площадь при разрыве, которая значительно меньше начальной вследствие образования шейки.
Характеристики пластичности
Напомним, что пластичность – это способность материала деформироваться без разрушения. Характеристики пластичности – деформационные, поэтому определяются по данным измерения образца после разрушения:
∆ℓос = ℓ1 - ℓ0 – остаточное удлинение,
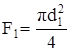 – площадь шейки.
– площадь шейки.
Относительное удлинение после разрыва:
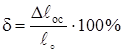 . (2.25)
. (2.25)
Эта характеристика зависит не только от материала, но и от соотношения размеров образца. Именно поэтому стандартные образцы имеют фиксированное отношение ℓ0 = 5d0 или ℓ0 = 10d0 и величина δ всегда приводится с индексом – δ5 или δ10, причём δ5 > δ10.
Относительное сужение после разрыва:
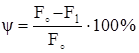 . (2.26)
. (2.26)
Удельная работа деформации:
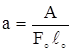 . (2.27)
. (2.27)
где А – работа, затраченная на разрушение образца; находится как площадь, ограниченная диаграммой растяжения и осью абсцисс (площадь фигуры OABCDKLMR). Удельная работа деформации характеризует способность материала сопротивляться ударному действию нагрузки.
Из всех полученных при испытании механических характеристик основными характеристиками прочности являются предел текучести σт и предел прочности σпч, а основными характеристиками пластичности – относительное удлинение δ и относительное сужение ψ после разрыва.
Разгрузка и повторное нагружение
При описании диаграммы растяжения было указано, что в точке К испытание остановили и произвели разгрузку образца. Процесс разгрузки описывался прямой KN (рис.2.16), параллельной прямолинейному участку OA диаграммы. Это означает, что удлинение образца ∆ℓ′П, полученное до начала разгрузки, полностью не исчезает. Исчезнувшая часть удлинения на диаграмме изображается отрезком NQ, оставшаяся – отрезком ОN. Следовательно, полное удлинение образца за пределом упругости состоит из двух частей – упругой и остаточной (пластической):
∆ℓ′П = ∆ℓ′уп + ∆ℓ′ос.
Так будет вплоть до разрыва образца. После разрыва упругая составляющая полного удлинения (отрезок ∆ℓуп) исчезает. Остаточное удлинение изображается отрезком ∆ℓос. Если же прекратить нагружение и разгрузить образец в пределах участка OB, то процесс разгрузки изобразится линией, совпадающей с линией нагрузки – деформация чисто упругая.
При повторном нагружении образца длиною ℓ0 + ∆ℓ′ос линия нагружения практически совпадает с линией разгрузки NK. Предел пропорциональности повысился и стал равным тому напряжению, от которого производилась разгрузка. Далее прямая NK перешла в кривую KL без площадки текучести. Часть диаграммы, расположенная левее линии NK, оказалась отрезанной, т.е. начало координат переместилось в точку N. Таким образом, в результате вытяжки за предел текучести, образец изменил свои механические свойства:
1). повысился предел пропорциональности;
2). исчезла площадка текучести;
3). уменьшилось относительное удлинение после разрыва.
Такое изменение свойств называется наклёпом.
При наклёпе повышаются упругие свойства и понижается пластичность. В некоторых случаях (например, при механической обработке) явление наклёпа нежелательно и его устраняют термообработкой. В других случаях его создают искусственно для улучшения упругости деталей или конструкций (обработка дробью рессор или вытяжка тросов грузоподъёмных машин).
Диаграммы напряжений
Чтобы получить диаграмму, характеризующую механические свойства материала, первичную диаграмму растяжения в координатах Р – ∆ℓ перестраивают в координатах σ – ε. Так как ординаты σ = Р/F и абсциссы σ = ∆ℓ/ℓ получают делением на постоянные, диаграмма имеет такой же вид, как и первоначальная (рис. 2.18,а).
а б
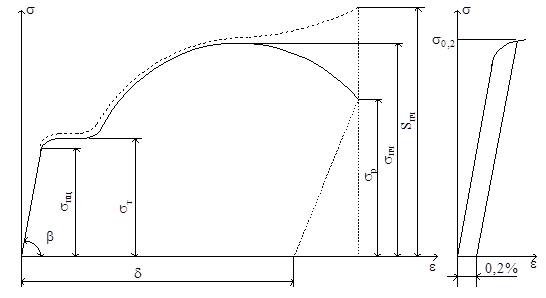
Из диаграммы σ – ε видно, что
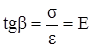 , (2.28)
, (2.28)
т.е. модуль нормальной упругости равен тангенсу угла наклона прямолинейного участка диаграммы к оси абсцисс.
По диаграмме напряжений удобно определять так называемый условный предел текучести. Дело в том, что большинство конструкционных материалов не имеет площадки текучести – прямая линия плавно переходит в кривую. В этом случае за величину предела текучести (условного) принимается напряжение, при котором относительное остаточное удлинение равно 0,2%. На рис. 2.18,б показано, как определяется величина условного предела текучести σ0,2. Предел текучести σт, определяемый при наличии площадки текучести, часто называют физическим.
Нисходящий участок диаграммы носит условный характер, поскольку действительная площадь поперечного сечения образца после образования шейки значительно меньше первоначальной площади, по которой определяются координаты диаграммы. Можно получить истинное напряжение, если величину силы в каждый момент времени Pt делить на действительную площадь поперечного сечения в этот же момент времени Ft:
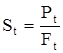 . (2.29)
. (2.29)
На рис. 2.18,а, этим напряжениям соответствует штриховая линия. До предела прочности S и σ практически совпадают. В момент разрыва истинное напряжение значительно превышает и предел прочности σпч и тем более напряжение в момент разрыва σр. Выразим площадь шейки F1 через ψ и найдем Sр.
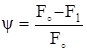 Þ
Þ 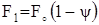 Þ
Þ 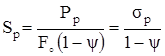 .
.
Для пластичной стали ψ = 50 – 65%. Если принять ψ = 50% = 0,5, то получим Sр = 2σр, т.е. истинное напряжение наибольшее в момент разрыва, что вполне логично.
2.6.2. Испытание на сжатие различных материалов
Испытание на сжатие дает меньше информации о свойствах материала, чем испытание на растяжение. Тем не менее, оно совершенно необходимо для характеристики механических свойств материала. Осуществляется на образцах в виде цилиндров, высота которых не более 1,5 диаметра, или на образцах в виде кубиков.
Рассмотрим диаграммы сжатия стали и чугуна. Для наглядности изобразим их на одном рисунке с диаграммами растяжения этих материалов (рис.2.19). В первой четверти – диаграммы растяжения, а в третьей – сжатия.
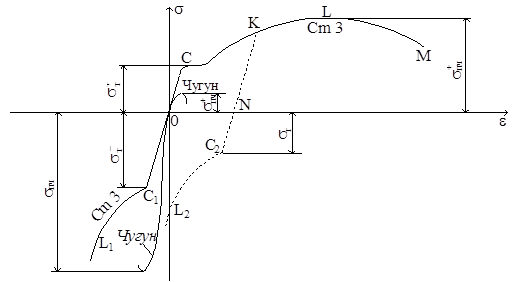
Рис.2.19
В начале загружения диаграмма сжатия стали – наклонная прямая с таким же наклоном, как и при растяжении. Потом диаграмма переходит в участок текучести (площадка текучести выражена не так отчетливо, как при растяжении). Далее кривая слегка изгибается и не обрывается, т.к. стальной образец не разрушается, а только сплющивается. Модуль упругости стали Е при сжатии и растяжении одинаков. Также одинаковы и предел текучести σт+ = σт-. Предел прочности при сжатии получить невозможно, как и невозможно получить характеристики пластичности.
Диаграммы растяжения и сжатия чугуна по форме похожи: искривляются с самого начала и по достижении максимальной нагрузки обрываются. Однако на сжатие чугун работает лучше, чем на растяжение (σпч- = 5 σпч+). Предел прочности σпч – это единственная механическая характеристика чугуна, получаемая при испытании на сжатие.
Трение, возникающее во время испытания между плитами машины и торцами образца, оказывает существенное влияние на результаты испытания и на характер разрушения. Цилиндрический стальной образец принимает бочкообразную форму (рис. 2.20,а), в чугунном кубике возникают трещины под углом 450 к направлению нагрузки. Если исключить влияние трения, смазав торцы образца парафином, трещины возникнут по направлению нагрузки и наибольшая сила будет меньше (рис.2.20,б и в). Большинство хрупких материалов (бетон, камень) разрушается при сжатии так же, как чугун, и имеет аналогичную диаграмму сжатия.
а б в г д
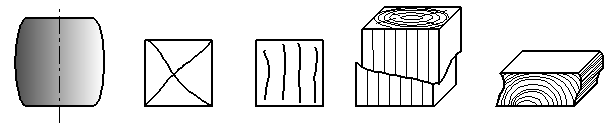
Рис.2.20
Представляет интерес испытание древесины – анизотропного, т.е. обладающего различной прочностью в зависимости от направления силы по отношению к направлению волокон, материала. Анизотропными являются и все более широко применяемые стеклопластики. При сжатии вдоль волокон древесина значительно прочнее, чем при сжатии поперек волокон (кривые 1 и 2 на рис.2.21). Кривая 1 похожа на кривые сжатия хрупких материалов. Разрушение происходит вследствие сдвига одной части кубика относительно другой (рис.2.20,г). При сжатии поперек волокон древесина не разрушается, а прессуется (рис. 2.20,д).
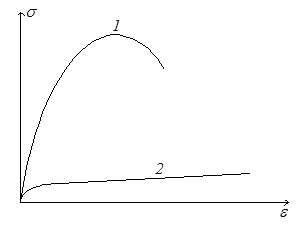
Рис.2.21
При испытании на растяжение стального образца мы обнаружили изменение механических свойств в результате вытяжки до появления заметных остаточных деформаций – наклёп. Посмотрим, как ведет себя образец после наклёпа при испытании на сжатие. На рис.2.19 диаграмма показана пунктиром. Сжатие идет по кривой NC2L2, которая располагается выше диаграммы сжатия образца, не подвергавшегося наклёпу OC1L1, и почти параллельно последней. После наклёпа растяжением пределы пропорциональности и текучести при сжатии уменьшаются. Это явление называется эффектом Баушингера по имени учёного, впервые его описавшего.
2.6.3. Определение твёрдости
Очень распространённым механико-технологическим испытанием является определение твёрдости. Это обусловлено быстротой и простотой таких испытаний и ценностью получаемой информации: твёрдостью характеризует состояние поверхности детали до и после технологической обработки (закалки, азотирования и т.п.), по ней можно косвенно судить о величине предела прочности.
Твёрдостью материала называется способность оказывать сопротивление механическому проникновению в него другого, более твёрдого тела. Величины, характеризующие твёрдость, называют числами твёрдости. Определяемые разными методами, они различны по величине и по размерности и всегда сопровождаются указанием способа их определения.
Наиболее распространённый метод – по Бринелю. Испытание заключается в том, что в образец вдавливают стальной закалённый шарик диаметра D (рис.2.22,а). Шарик выдерживается некоторое время под нагрузкой P, в результате чего на поверхности остается отпечаток (лунка) диаметром d. Отношение нагрузки в кН к площади поверхности отпечатка в см2 называется числом твёрдости по Бринелю
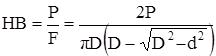 . (2.30)
. (2.30)
Для определения числа твёрдости по Бринелю используют специальные испытательные приборы, диаметр отпечатка измеряется портативным микроскопом. Обычно HB не считают по формуле (2.30), а находят из таблиц.
а б

Пользуясь числом твёрдости HB, можно без разрушения образца получить приближённое значение предела прочности некоторых металлов, т.к. существует линейная связь между σпч и HB: σпч = k ∙ HB (для малоуглеродистой стали k = 0,36, для высокопрочной стали k = 0,33, для чугуна k = 0,15, для алюминиевых сплавов k = 0,38, для титановых сплавов k = 0,3).
Весьма удобен и широко распространён метод определения твердости по Роквеллу. В этом способе в качестве индентора, вдавливаемого в образец, используется алмазный конус с углом при вершине 120 градусов и радиусом закругления 0,2 мм, или стальной шарик диаметром 1,5875 мм (1/16 дюйма). Испытание происходит по схеме, приведённой на рис. 2.22,б. Сначала конус вдавливается предварительной нагрузкой P0 = 100 H, которая не снимается до конца испытания. При этой нагрузке конус погружается на глубину h0. Затем на конус подается полная нагрузка P = P0 + P1 (два варианта: A – P1 = 500 H и C – P1 = 1400 H), при этом глубина вдавливания увеличивается. После снятия основной нагрузки P1 остается глубина h1. Глубина отпечатка, полученная за счёт основной нагрузки P1, равная h = h1 – h0, характеризует твердость по Роквеллу. Число твёрдости определяется по формуле
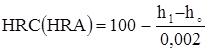 , (2.31)
, (2.31)
где 0,002 – цена деления шкалы индикатора твердомера.
Существуют и другие методы определения твёрдости (по Виккерсу, по Шору, микротвёрдость), которые здесь не рассматриваются.
2.6.4. Сравнение свойств различных материалов
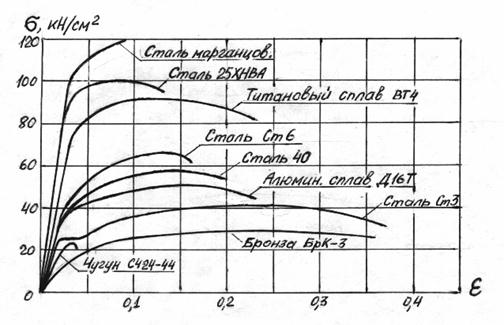 |
Мы уже подробно рассмотрели свойства пластичного и хрупкого материалов – малоуглеродистой стали и серого чугуна - при растяжении и сжатии. Продолжим это сравнение – рассмотрим диаграммы растяжения некоторых металлов (рис.2.23).
Рис.2.23
Все показанные на рисунке стали –40, Ст6, 25ХНВА, марганцовистая – имеют гораздо более высокие характеристики прочности, чем малоуглеродистая сталь Ст3. Площадка текучести у высокопрочных сталей отсутствует, относительное удлинение при разрыве δ значительно меньше. За повышение прочности приходится платить понижением пластичности. Хорошей пластичностью обладают алюминиевый и титановый сплавы. При этом прочность алюминиевого сплава выше, чем у Ст3, а объёмный вес почти в три раза меньше. А титановый сплав имеет прочность на уровне высокопрочной легированной стали при почти в два раза меньшем объемном весе. В табл.2.4 приведены механические характеристики некоторых современных материалов.
| Материал | Марка | Предел текучести, σт | Предел прочности, σпч | Относит. удлинение при разрыве, δ5 | Относит сужение при разрыве, ψ | Объёмный вес, γ | Модуль Юнга, E |
| кН/см2 | кН/см2 | % | % | г/см3 | кН/см2 | ||
| Сталь углеродистая горячекатаная | Ст3 | 34-42 | 7,85 | 2·104 | |||
| Сталь углеродистая горячекатаная | СТ6 | 60-72 | 7,85 | 2·104 | |||
| Сталь углеродистая качественная | 7,85 | 2·104 | |||||
| Сталь легированная хромникельвольфрамовая | 25ХНВА | 7,85 | 2,1·104 | ||||
| Сталь легированная кремнехроммарганцовистая | 35ХГСА | 7,85 | 2,1·104 | ||||
| Чугун | СЧ24-44 | - | 
| - | - | 7,85 | 1,5·104 |
| Алюминиевый сплав | Д16Т | - | 2,8 | 0,7·104 | |||
| Бронза кремнистая | БрК-3 | - | - | 7,85 | 1,1·104 | ||
| Титановый сплав | ВТ4 | - | 4,5 | ||||
| Стеклопластик | СВАМ | - | - | 1,9 | 0,4·104 | ||
| Углепластик | КЕВЛАР | - | - | 1,7 | 3·104 |
В последних двух строчках таблицы приведены характеристики полимерных композиционных материалов, отличающихся малым весом и высокой прочностью. Особо выдающимися свойствами отличаются композиты на основе суперпрочных углеродных волокон – прочность их примерно в два раза выше прочности самой лучшей легированной стали и на порядок – малоуглеродистой стали. Они жестче стали в полтора раза и легче почти в пять раз. Применяются, конечно, в военной технике – авиа- и ракетостроении. В последние годы начинают применяться и в гражданских областях – автомобилестроении (кузова, тормозные диски, выхлопные трубы гоночных и дорогих спортивных машин), судостроении (корпуса катеров и малых судов), медицине (инвалидные коляски, детали протезов), машиностроении для спорта (рамы и колеса гоночных велосипедов и другой спортивный инвентарь). Широкому применению этого материала пока препятствует его высокая стоимость и низкая технологичность.
Резюмируя все вышесказанное о механических свойствах различных материалов, можно сформулировать основные особенности свойств пластичных и хрупких материалов.
1. Хрупкие материалы, в отличие от пластичных, разрушаются при незначительных остаточных деформациях.
2. Пластичные материалы одинаково сопротивляются растяжению и сжатию, хрупкие – хорошо сжатию и плохо растяжению.
3. Пластичные материалы хорошо сопротивляются ударным нагрузкам, хрупкие – плохо.
4. Хрупкие материалы очень чувствительные к так называемой концентрациинапряжений (локальным всплескам напряжений вблизи мест резкого изменения формы деталей). На прочность деталей из пластичного материала концентрация напряжений влияет в гораздо меньшей степени. Более подробно об этом – чуть ниже.
5. Хрупкие материалы не поддаются технологической обработке, связанной с пластической деформацией – штамповке, ковке, волочению и т.п.
Деление материалов на пластичные и хрупкие носит условный характер, так как при некоторых условиях хрупкие материалы получают пластические свойства (например, при большом всестороннем сжатии) и, наоборот, пластичные материалы приобретают хрупкие свойства (например, мягкая сталь при низкой температуре). Поэтому правильнее говорить не о пластичном и хрупком материалах, а об их пластическом и хрупком разрушении.
Как уже указывалось, детали машин и других конструкций должны удовлетворять условиям прочности (2.3) и жёсткости (2.13). Величина допускаемых напряжений устанавливается в зависимости от материала (его механических характеристик), вида деформации, характера действия нагрузок, условий работы конструкций и тяжести последствий, которые могут наступить в случае разрушения:
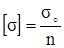 , (2.32)
, (2.32)
где σ0 – напряжение, соответствующее наступлению опасного состояния для данного материала;
n – коэффициент запаса прочности, n > 1.
Для деталей, выполненных из пластичного материала, опасное состояние характеризуется появлением больших остаточных деформаций, поэтому опасное напряжение равно пределу текучести σоп = σт.
Для деталей, изготовленных из хрупкого материала, опасное состояние характеризуется появлением трещин, поэтому опасное напряжение равно пределу прочности σоп = σпч.
Все перечисленные выше условия работы деталей учитываются коэффициентом запаса прочности. При любых условиях имеют место некоторые общие факторы, учитываемые коэффициентом запаса прочности:
1. Неоднородность материала, следовательно, разброс механических характеристик;
2. Неточность задания величин и характера внешних нагрузок;
3. Приближённость расчётных схем и методов расчёта.
На основании данных длительной практики конструирования, расчёта и эксплуатации машин и сооружений величина коэффициента запаса прочности для стали принимается равной 1,4 – 1,6. Для хрупких материалов при статической нагрузке принимают запас прочности 2,5 – 3,0. Итак, для пластичных материалов:
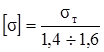 . (2.33)
. (2.33)
Для хрупких материалов
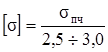 . (2.34)
. (2.34)
При сравнении свойств пластичных и хрупких материалов отмечалось, что на прочность влияет концентрация напряжений. Теоретические и экспериментальные исследования показали, что равномерное распределение напряжений по площади поперечного сечения растянутого (сжатого) стержня в соответствии с формулой (2.2) нарушается вблизи мест резкого изменения формы и размера поперечного сечения – отверстий, галтелей, выкружек и др. Около этих мест возникают локальные всплески напряжений – концентрация напряжений.
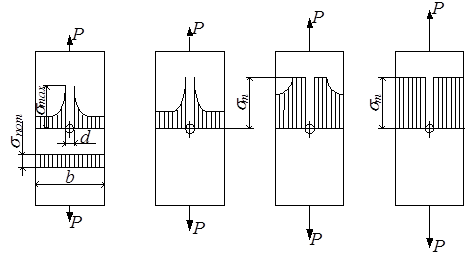
Для примера рассмотрим концентрацию напряжений в растягиваемой полосе с малым отверстием. Отверстие считается малым, если выполняется условие d ≤ 1/5b (рис.2.27,а). При наличии концентрации напряжение определяется по формуле:
σmax = ασ∙ σnom. (2.35)
где ασ – коэффициент концентраций напряжений, определяемый методами теории упругости или экспериментально на моделях;
σnom – номинальное напряжение, т.е. напряжение, вычисленное для данной детали при отсутствии концентрации напряжений.
Для рассматриваемого случая (ασ = 3 и σnom = N/F) эта задача является в известном смысле классической задачей о концентрации напряжений и называется по имени решившего её в конце XIX века учёного задачей Кирша.
Рассмотрим, как поведет себя полоса с отверстием по мере увеличения нагрузки. В пластичном материале максимальное напряжение у отверстия станет равным пределу текучести (рис.2.27,б). Концентрация напряжений всегда очень быстро затухает, поэтому уже на небольшом удалении от отверстия напряжение гораздо меньше. Увеличим нагрузку (рис.2.27,в): напряжение у отверстия не увеличивается, т.к. пластичный материал имеет довольно протяжённую площадку текучести, уже на некотором удалении от отверстия напряжение становится равным пределу текучести.
а б в г
 2014-02-24
2014-02-24 4748
4748
