3.1. Компоненты напряжений. Виды напряжённых состояний
Центральное растяжение или сжатие бруса является самым простым видом деформации тела, когда напряжение во всех его точках одинаково (однородное напряжённое состояние). В произвольным образом нагруженном теле (рис.3.1,а) напряжение меняется от точки к точке и поэтому в произвольном сечении m-n этого тела напряжения распределены неравномерно. В этом случае при изучении распределения напряжений в окрестности произвольной точки K рассматриваемого сечения m-n мысленно вырезают бесконечно малый параллелепипед (рис.3.1,б). Ввиду его малости можно считать, что по граням напряжения распределены равномерно. На рис.3.1,в показаны напряжения, действующие по граням бесконечно малого параллелепипеда.
а б в
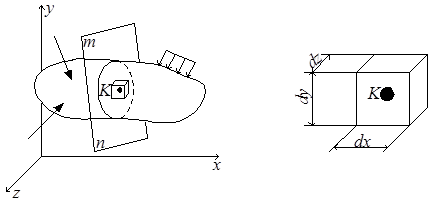
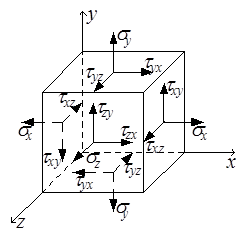
Рис.3.1
σх – нормальное напряжение, действующее по направлению оси x; положительное при растяжении, отрицательное при сжатии;
τху – касательное напряжение, действующее по площадке с нормалью х (первый индекс) в направлении оси у (второй индекс); положительно, если стремится развернуть элемент по часовой стрелке (глядя со стороны положительного направления оси).
На рис.3.1,в нормальные напряжения σх, σу и σz положительные, касательные напряжения τху < 0, τух > 0. Под действием приложенных к нему напряжений элемент должен находиться в равновесии, следовательно, для него можно записать уравнения статики. Покажем напряжения, дающие момент относительно оси OZ (рис.3.2) и запишем соответствующее уравнение статики:
∑ Moz = 0: 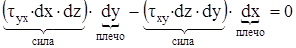 ; (3.1)
; (3.1)
τух = τху..

Рис.3.2
Учитывая правило знаков, перепишем формулу (3.1)
τху = – τух, τzx = – τxz, τ zy = – τyz. (3.2)
Формула (3.2) выражает закон парности касательных напряжений: на любых взаимно перпендикулярных площадках касательные напряжения с одноимёнными индексами равны по величине и вращают элемент в противоположные стороны.
Таким образом, шесть независимых компонентов напряжений σх, σу, σz, τху, τух, τzx – характеризуют напряжённое состояние в точке.
Напряжённым состоянием в точке называется совокупность напряжений, действующих по всевозможным площадкам, проведённым через эту точку.
При повороте бесконечно малого параллелепипеда меняются компоненты напряжённого состояния. Всегда можно найти такое его положение, что по граням (площадкам) параллелепипеда будут действовать только нормальные напряжения. Такие площадки называются главными, а нормальные напряжения, по ним действующие, называются главными нормальными напряжениями (рис.3.3).
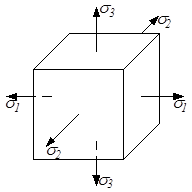
Рис.3.3
Это положение доказывается в теории упругости. Главные нормальные напряжения принято обозначать цифровыми индексами по следующему правилу: σ1 > σ2 > σ3. Соблюдение этого правила важно с точки зрения расчёта на прочность. Например: три главных напряжения имеют значения 120 МПа, – 50МПа и – 30 МПа; их надо записать σ1 = 120 МПа, σ2 = – 30 МПа и σ3 = – 50 МПа.
Напряжённое состояние в точке классифицируется на три вида: линейное (одноосное), плоское (двухосное) и объёмное (трёхосное) в зависимости от того, испытывает ли параллелепипед растяжение (сжатие) в одном, двух или трёх взаимно перпендикулярных направлениях (рис.3.4).
а б в
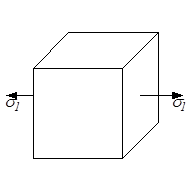
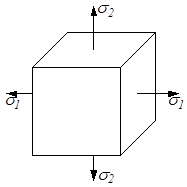
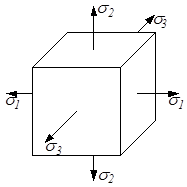
Рис.3.4
3.2. Линейное напряжённое состояние
Линейное напряжённое состояние имеет место в стержнях, испытывающих растяжение или сжатие, а также в некоторых точках стержня, работающего на изгиб. Рассмотрим растяжение стержня. Как указывалось в главе 2, в поперечных сечениях, удалённых от точек приложения внешних сил, нормальные напряжения распределены равномерно и равны (рис.3.5,а)
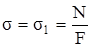 . (3.3)
. (3.3)
Эти напряжения являются главными, т.к. касательные напряжения в поперечном сечении равны нулю. Напряжённое состояние при растяжении является однородным, поэтому размеры выделяемых элементов не играют никакой роли. Определим напряжения, действующие по наклонной площадке. Наклон площадки определяется острым углом α между направлением оси стержня и нормалью nα к площадке. Условимся считать угол α положительным, если он отсчитывается против часовой стрелки (рис.3.5,а). Элемент, находящийся в линейном напряжённом состоянии, изображаем в виде плоской фигуры, помня, однако, что в действительности он имеет вид, показанный на рис.3.4,а.
Рассмотрим равновесие нижней части стержня, отсечённой наклонной площадкой (рис.3.5,б). По наклонной площадке, площадь которой равна Fα, равномерно распределены напряжения pα, параллельные осевой силе N = P, следовательно, результирующая этих напряжений
pαFα = N.
Отсюда найдём pα, подсчитав предварительно 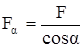
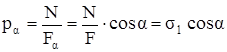 .
.
Проектируя pα на нормаль nα и на плоскость сечения, получим выражения для нормальных и касательных напряжений по наклонной площадке:
σα = pαcos α, τα = pαsin α
или
σα = σ1cos2α. (3.4)
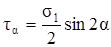 . (3.5)
. (3.5)
а б в
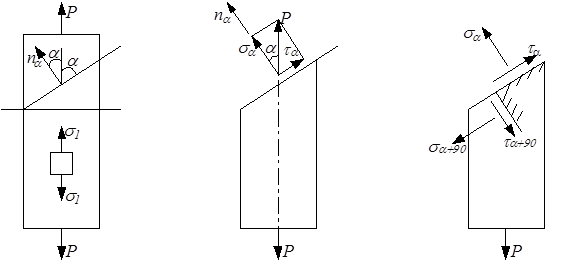
Рис.3.5
Как видно из формул (3.4) и (3.5), при α = 0 ® τα = 0 и σα = σ1, при α = π/2 ® σα = 0 и τα = 0. Таким образом, при растяжении действительно имеет место линейное напряжённое состояние: σ1 = N/F, σ2 = σ3 = 0. При сжатии σ3 = – N/F, σ1 = σ2 = 0.
Из выражения (3.5) видно, что касательные напряжения достигают своей наибольшей величины при α = ± 450, причём
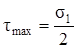 . (3.6)
. (3.6)
Определим теперь напряжения, действующие по площадке, перпендикулярной заданной наклонной, α1 = α + 900 (рис.3.5,в):
σα1 = σ1 ∙ cos2 (α + 90) = σ1sin2 α,
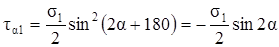 .
.
Итак
σα+90 = σ1sin2 α. (3.7)
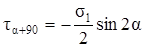 . (3.8)
. (3.8)
3.3. Плоское напряжённое состояние
Плоское напряжённое состояние встречается в деталях машин и в строительных конструкциях очень часто. Например, это стержень при кручении (рис.3.6,а) и изгибе (рис.3.6,б), тонкостенный сосуд под действием внутреннего давления (рис.3.6,в).
а б в

Рис.3.6
Плоское напряжённое состояние также имеет место в тонкой пластине, нагруженной силами, параллельными её плоскости и равномерно распределёнными по толщине (рис.3.7): σх ≠ 0, σу ≠ 0, τху ≠ 0, σz = τzx = τzy = 0.
Рассмотрим два аспекта задачи о плоском напряжённом состоянии: найдём напряжения, действующие по наклонной площадке (прямая задача), и найдём величины и направления главных напряжений (обратная задача).
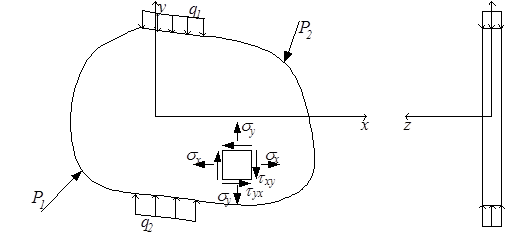
Рис.3.7
3.3.1. Прямая задача
Дано: напряжения σх, σу, τху, угол α > 0 (рис.3.8,а).
Определить: напряжения σα и τα (рис.3.8,б).
Рассмотрим равновесие элемента abc. При записи уравнений статики будем определять силу как произведение напряжения на площадь соответствующей грани:
площадь наклонной грани bc = dF;
площадь прямой грани ab = dF ∙ cos α;
площадь прямой грани ac = dF ∙ sin α..
а б в
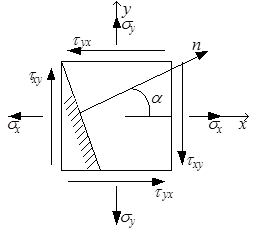


Рис.3.8
Теперь запишем уравнения проекций всех сил, действующих на элемент abc, на нормаль к наклонной площадке и на ось, совпадающую с этой площадкой (рис.3.8,в).
∑n = 0: σαdF – σx dF cos α ∙ cos α – σу dF sin α ∙ sin α + τxу dF cos α ∙ sin α + τух dF sin α ∙ cos α = 0,
∑t = 0: ταdF + σу dF sin α ∙ cos α + τуx dF sin α ∙ sin α – τxу dF cos α ∙ cos α – σх dF cos α ∙ sin α = 0.
После несложных преобразований и сокращения на dF получаем следующие выражения:
σα = σх cos2α + σy sin2α – τxy sin 2α, (3.9)
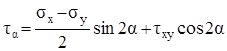 . (3.10)
. (3.10)
Если исходные площадки являются главными (рис.3.9), то формулы (3.9) и (3.10) упрощаются:
σα = σ1cos2α + σ2sin2, (3.11)
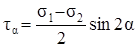 . (3.12)
Из формулы (3.12) следует, что наибольшее касательное напряжение действует по площадке, наклонённой под углом 450 к главным площадкам: . (3.12)
Из формулы (3.12) следует, что наибольшее касательное напряжение действует по площадке, наклонённой под углом 450 к главным площадкам:
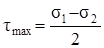 . (3.13) . (3.13)
| 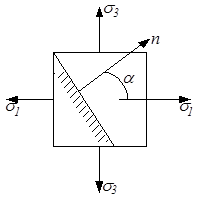 Рис.3.9
Рис.3.9
|
Преобразуем формулу (3.9), используя выражение для тригонометрических функций
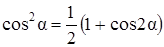 и
и 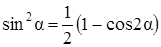 .
.
Получим
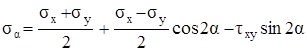 . (3.14)
. (3.14)
Теперь определим напряжения, действующие по площадке, перпендикулярной к заданной: α1 = α + 900. Воспользуемся формулой (3.14), учитывая, что cos 2α1 = – cos 2α и sin 2α1 = – sin 2α. Получим
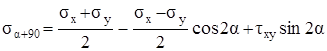 . (3.15)
. (3.15)
Сложим (3.14) и (3.15), чтобы найти сумму нормальных напряжений, действующих по взаимно перпендикулярным площадкам.
Получим
σα + σα + 90 = σх + σу = const, (3.16)
т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам инвариантна по отношению к наклону этих площадок.
3.3.2. Обратная задача
Дано: напряжения σх, σу, τху (рис.3.8,а).
Определить: положение главных площадок и величины главных напряжений σ1 и σ2.
По определению на главных площадках τα = 0. Из формулы (3.10) найдём угол α0 между осью х и одним из главных напряжений.
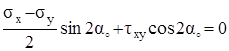 ,
,
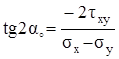 . (3.17)
. (3.17)
Величины главных напряжений можно найти по формулам (3.14) и (3.15), подставив в них α0. Удобнее иметь формулы для главных напряжений, не зависящие от углов и тригонометрических функций. Для вывода используем зависимости косинуса и синуса двойного угла от тангенса
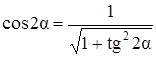 ,
, 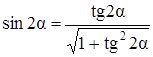 .
.
Подставим их в формулу (3.14):
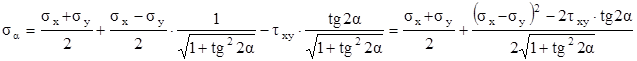 . (*)
. (*)
Теперь в выражение (*) подставим tg 2α0 по формуле (3.17) и получим значение большего главного напряжения
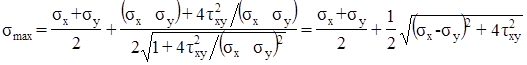 .
.
Второе главное напряжение получим, используя формулу (3.15). В результате выражение для главных напряжений при плоском напряжённом состоянии имеет следующий вид:
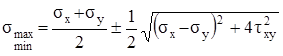 . (3.18)
. (3.18)
Для определения σmax после первого слагаемого ставим «+», а для определения σmin ставим «–». Следует обратить внимание на то, что если одно из главных напряжений, вычисленных по формуле (3.18), окажется отрицательным, то их следует обозначить σ1 и σ3. Если же оба главных напряжений окажутся отрицательными, то σ2 и σ3; оба положительными, то σ1 и σ2.
Главные напряжения обладают свойством экстремальности – одно из них наибольшее, другое – наименьшее из всех возможных в данной точке тела (помним о том, что сумма нормальных напряжений на взаимно перпендикулярных площадках постоянна). Для доказательства исследуем на экстремум функцию σα (формула 3.9). Продифференцируем её и приравняем производную нулю.
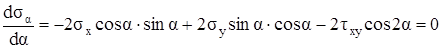 ®
®
® – 2τxy cos 2α = (σx – σy)sin 2α ® 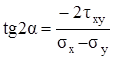 .
.
Площадки, характеризуемые этими углами, являются главными в соответствии с формулой (3.17).
3.4. Объёмное напряжённое состояние. Общие понятия
Объёмное напряжённое состояние встречается реже, чем плоское. Пример – толстостенный сосуд давления (рис.3.10). Подробным образом изучают объёмное напряжённое состояние в курсе теории упругости, в сопротивлении материалов – только основные понятия.
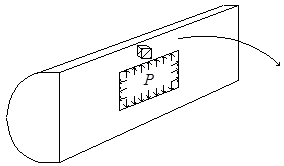
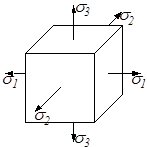
Рис.3.10
Рассмотрим объёмное напряжённое состояние, заданное главными напряжениями (рис.3.11).

Рис.3.11
Напряжения, действующие по наклонной площадке с нормалью n, находятся по формулам
σα = σ1cos2α1 + σ2cos2α2 + σ3cos2α3, (3.19)
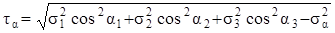 . (3.20)
. (3.20)
Эти формулы приведены без вывода. В них α1, α2, α3 – углы, которые образуют нормаль к площадке n с осями x, y, z соответственно.
Если наклонная площадка параллельна одному из главных напряжений, то напряжения, по ней действующие, не зависят от этого главного напряжения. Они определяются по формулам плоского напряженного состояния в зависимости от двух других главным напряжений. Учитывая, что главные напряжения экстремальные, т.е. σ1 = σmax и σ3 = σmin, легко найти наибольшее касательное напряжение. Очевидно, оно действует по площадке, параллельной σ2 и наклоненной под углом 450 к σ1 и σ3 (рис.3.12). Определяется формулой (3.13)
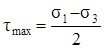 . (3.21)
. (3.21)
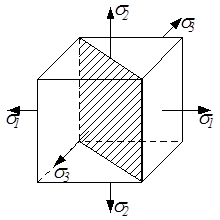
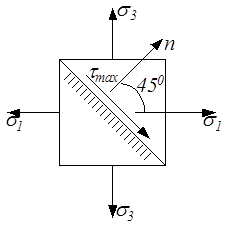
Рис.3.12
Известный интерес, особенно при изучении пластических деформаций, представляют напряжения, действующие по площадке, равнонаклонённой ко всем главным направлениям. Такая площадка называется октаэдрической, поскольку она параллельна грани октаэдра, который может быть образован из куба. Нормаль к этой площадке образует равные углы с главными направлениями:
α1 = α2 = α3 = α.
Учитывая, что всегда
cos2α1 + cos2α2 + cos2α3 = 1,
Получаем
cos2α = ⅓.
Тогда из формул (3.19) и (3.20) находим
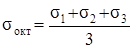 , (3.22)
, (3.22)
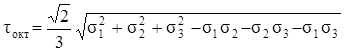 . (3.23)
. (3.23)
При изучении вопросов прочности деформация бесконечно малого элемента разделяется на деформацию изменения объёма и деформацию искажения формы. Оказывается, что σокт «ответственно» за изменение объёма, а τокт – за изменение формы.
Напряжение σокт представляет собой среднее напряжение для данного объемного напряженного состояния, σокт = σср
3.5.Деформации при объёмном напряжённом состоянии.
 2014-02-24
2014-02-24 4736
4736
