Таблица 2.3
Рис.2.14
Рис.2.9
Статически неопределимые системы
Мы рассмотрели два примера, в которых внутренние усилия в стержнях определялись из уравнений статики. Это были статически определимые системы.
Статически определимыми называются системы, у которых число неизвестных реакций (число внутренних силовых факторов) равно числу уравнений статики.
Рассмотренные конструкции легко можно переделать – с целью повышения прочности установить дополнительную опору или дополнительный стержень (рис.2.9).
а б
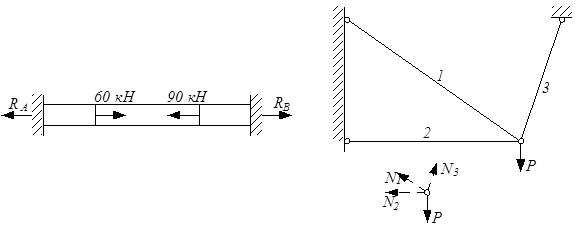
При этом увеличивается число неизвестных усилий, а число уравнений статики остается неизменным. Так, для стержня на рис.2.9,а невозможно найти две неизвестных опорных реакции RA и RВ (и, соответственно, продольную силу N на каждом из трёх участков) из единственного уравнения статики ∑ х = 0. А для кронштейна на рис.2.9,б невозможно найти усилия в стержнях N1, N2 и N3 из двух уравнений статики. Конструкции стали статически неопределимыми.
Статически неопределимыми называются системы, у которых число неизвестных реакций (число внутренних силовых факторов) превышает число уравнений статики. Разность между числом неизвестных усилий и числом независимых уравнений статики называется степенью статической неопределимости. Её можно найти из таких соображений: степень статической неопределимости равна числу “лишних” связей – связей, которые можно удалить из конструкций без ущерба для статического равновесия. Например, абсолютно жёсткий брус АВ закреплен на шарнирной опоре А и удерживается четырьмя тягами (рис.2.10). Равновесие бруса АВ не будет нарушено, если из четырех тяг удалить три. Если же удалить все четыре, конструкция превратится в механизм – брус АВ упадёт. Поэтому степень статической неопределённости этой системы равна трём. Для системы, показанной на рис.2.9, степень статической неопределённости равна единице. Степень статической неопределённости ничем не ограничена.

Рис.2.10
Недостающие для определения усилий уравнения могут быть получены из рассмотрения деформации системы.
Статически неопределимые конструкции, элементы которых работают на растяжение и сжатие, будем рассчитывать, придерживаясь следующего порядка.
1. Статическая сторона задачи. Составляем уравнения равновесия отсечённых элементов конструкций, содержащие неизвестные усилия.
2. Геометрическая сторона задачи. Рассматривая систему в деформированном состоянии, устанавливаем связи между деформациями или перемещениями отдельных элементов конструкции. Полученные уравнения называются уравнениями совместности деформаций.
3. Физическая сторона задачи. На основании закона Гука выражаем деформации элементов конструкций через действующие в них неизвестные усилия. В случае изменения температуры к деформациям, вызванным усилиями, добавляются температурные деформации.
4. Синтез. Решая совместно статические и геометрические уравнения, выраженные через физические, находим неизвестные усилия.
5. Расчёт на прочность. Из условия прочности стержней, в зависимости от поставленной задачи, находим площади поперечного сечения стержней или действующие напряжения для проверки прочности, или грузоподъёмность конструкции.
Рассмотрим примеры расчёта простых статически неопределённых конструкций.
2.5.1. Расчёт на действие нагрузки
Подобрать площади поперечного сечения стержней трёхстержневой фермы, изображённой на рис.2.11,а.
а б
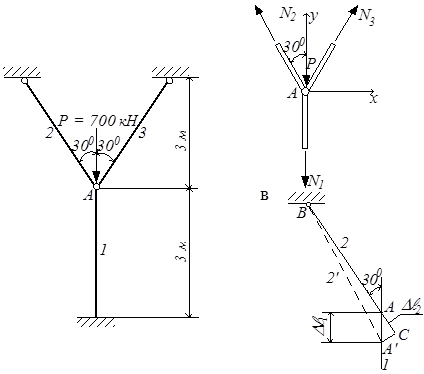
Рис.2.11
Поскольку при расчёте статически неопределённых конструкций используются уравнения совместности деформаций, выражаемые по закону Гука через жёсткость EF, а значения F нам неизвестны, необходимо заранее задавать соотношение площадей рассчитываемых стержней. Исходные данные – в табл.2.1.
Таблица 2.1.
| Стержень | Площадь поперечного сечения F | Модуль Юнга E, кН/см2 | Допускаемое напряжение [σ], кН/см2 |
| F1 | 104 | ||
| 2F1 | 2·104 |
Определим длины стержней:
ℓ1 = 3 м, ℓ2 = ℓ3 = 3/cos 300 = 3/0,866 = 3,46 м ® ℓ2 = 3,46 м.
Решаем задачу в соответствии с записанным выше порядком расчёта.
1. Условия равновесия узла А (рис.2.11,б) выражаются двумя уравнениями статики:
∑ х = 0: N3sin 300 – N2sin 300 = 0 ® N3 = N2,
∑ у = 0: N1 + P – N2cos 300 – N3cos 300 = 0.
В результате остается одно второе уравнение, содержащее два неизвестных усилия:
N1 + P – 2N2cos 300 = 0. (a)
Таким образом, конструкция один раз статически неопределима.
2. Так как система симметрична относительно оси среднего стержня и боковые стержни растягиваются одинаковыми силами, то узел A опустится по вертикали на величину деформации первого стержня ∆ℓ1 и займёт положение A′ (рис.2.11,в). Стержни 2 и 3 удлиняются, на рисунке показан только второй стержень ВА и его новое положение ВА′. Удлинение бокового стержня получим, если из точки В радиусом, равным ВА′, проведём дугу и сделаем засечку на старом положении стержня ВА. Вследствие малости упругих удлинений по сравнению с длинами стержней можно дугу заменить перпендикуляром А′С, опущенным на линию АВ: АС = ∆ℓ2. Из рисунка:
∆ℓ2 = ∆ℓ1cos 300. (б)
Уравнение (б) есть уравнение совместности деформаций.
3. Удлинения стержней выразим по закону Гука через действующие в них усилия:
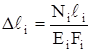 .
.
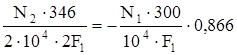 ® 86,5 N2 = – 259,8 N1 ® N1 = – 0,33N2. (в)
® 86,5 N2 = – 259,8 N1 ® N1 = – 0,33N2. (в)
Деформация 1-го стержня записана со знаком ''–'' т.к. она – укорочение.
4. Необходимо решить совместно уравнение статики (а) и уравнение совместности деформаций, выраженное через усилия (в):
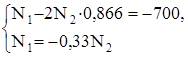
В результате решения системы уравнений получим:
N1 = – 112,1 кН, N2 = 339,5 кН.
Найдём площади поперечного сечения стержней из условия прочности 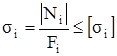 :
:
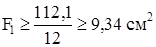 ,
, 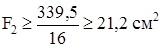 . (г)
. (г)
Так как кроме условий (г) должно еще выполняться первоначально заданное соотношение F2 = 2F1, окончательно принимаем: F1 = 10,6 см2, F2 = 21,2 см2. При этом напряжение во втором стержне будет равно допускаемому, а в первом оно будет меньше допускаемого
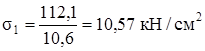 .
.
Отметим, что в статически неопределимых конструкциях невозможно получить равнопрочность всех элементов – всегда есть недогруженные стержни.
2.5.2. Температурные напряжения
В элементах статически неопределимых конструкций при изменении температуры возникают усилия (напряжения). Статически определимые конструкции при изменении температуры деформируются свободно: если нагреть стержень на ∆Т градусов, то он удлинится (рис.2.12) на величину ∆ℓТ.

Рис.2.12
∆ℓТ = α ∙ ∆Т ∙ ℓ, (2.19)
где α – коэффициент линейного расширения, размерность – 1/ град.
Превратим стержень, показанный на рис.2.12, в статический неопределимый. Для этого справа установим жёсткую опору (рис.2.13).

Рис.2.13
Теперь при нагревании жёсткие опоры препятствуют удлинению стержня, в результате чего возникают реакции, направленные вдоль оси. Уравнение статики:
∑ х = 0: RB – RA = 0 ® RB = RA = R.
Уравнение совместности деформаций:
∆ℓ = ∆ℓТ + ∆ℓN = 0.
Записываем физическое уравнение, помня о том, что обе составляющие имеют знак “ + “, т.к. продольная сила N = R – растягивающая и от нагревания стержень должен удлиняться:
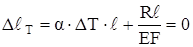 .
.
Получаем формулу для напряжения в стержне при равномерном по длине нагреве
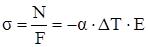 . (2.20)
. (2.20)
Теперь вернёмся к ферме, показанной на рис.2.11, и определим напряжения, возникающие в её стержнях, при равномерном нагреве одного из них. Внешняя сила Р при этом отсутствует. Исходные данные – в табл.2.2. Узел А – на рис.2.11,б, Р = 0.
Таблица 2.2.
| Стержень | Площадь поперечного сечения F, см2 | Коэффициент линейного расширения α, 1/град | Изменение температуры ∆Т0, С | |||
| 10,6 | 225·10-7 | +40 | ||||
| 21,2 | ||||||
| 1. | ∑ х = 0: N3sin 300 – N2sin 300 = 0 ® N3 = N2, ∑ у = 0: N1 – 2N2cos 300 = 0. | а) | ||||
2. Схема деформации – на рис.2.11,в, уравнение совместности деформации остается то же самое
∆ℓ2 = ∆ℓ1 ∙ cos 300. (б)
3. Физическая сторона задачи:
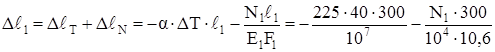 ,
,
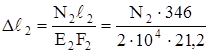 .
.
В первом уравнении поставим знаки “–“, т.к. на схеме деформации системы первый стержень укорачивается. Теперь выражения для ∆ℓ подставляем в уравнение совместности деформаций (б):
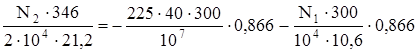 .
.
Получили 8,16N2 + 24,5N1 = – 2338,2. (в)
4. Синтез. Решаем систему уравнений (а) и (в):
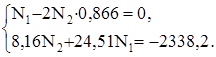
Получаем N1 = – 80 кН, N2 = – 46,26 кН.
5. Расчёт на прочность:
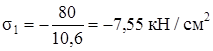 ,
, 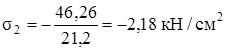 .
.
Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.
2.5.3. Монтажные напряжения
Свободная сборка статически неопределимых конструкций возможна при точном изготовлении их элементов. При отклонении размеров элементов от номинальных сборку можно осуществить с приложением усилий, вызывающих деформации элементов, поэтому в них после монтажа системы будут напряжения, называемые начальными или монтажными. В статически определимых конструкциях неточность размеров элементов не требует применения усилий при монтаже, и в элементах не возникают начальные напряжения.
Снова рассмотрим трёхстержневую статически неопределимую ферму и определим монтажные напряжения при условии, что длина первого стержня оказалась короче номинальной на величину δ (рис.2.14 и табл.2.3).
а б

| Стержень | Площадь поперечного сечения F, см2 | Модуль Юнга E, кН/см2 | Неточность изготовления δ, см |
| 10,6 | 104 | -0,3 | |
| 21,2 | 2·104 |
Если величина δ незначительна по сравнению с длинами стержней, то приложив определенные усилия, можно все три стержня соединить в узле, который займёт положение А′ (рис.2.14,б). Очевидно, при этом все стержни будут растянуты, поэтому схема сил на рис. 2.11, б (Р = 0).
1. Статическая сторона этой задачи совпадает со статической стороной задачи о температурных напряжениях. Уравнения статики те же самые:
| ∑х = 0: N3sin 30 – N2sin30 = 0, N3= N2, ∑y = 0: N1 – 2N2cos30 = 0. | (а) |
2. Геометрическая сторона задачи. Из приведённой на рис.2.14,б схемы деформации следует уравнение совместности деформаций
∆ℓ2 = (δ – ∆ℓ1) ∙ cos 30. (б)
3. Физическая сторона задачи. По закону Гука
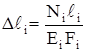 ,
,
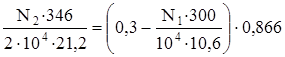 Þ 8,16 N2 = 2598 – 24,51 N1. (в)
Þ 8,16 N2 = 2598 – 24,51 N1. (в)
Следует отметить, что при записи уравнения совместности деформаций величину δ необходимо подставлять со знаком “+ “, т.к. знак “ - “ в таблице исходных данных – это лишь условное обозначение того обстоятельства, что длина стержня короче номинальной. В схеме деформации на рис.2.14,б и соответственно в уравнении совместности деформаций (б) это обстоятельство учтено.
4. Синтез. Решаем систему уравнений (а) и (б):
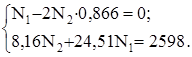
Получаем N1 = 88,81 кН, N2 = 51,33 кН.
5. Расчёт на прочность
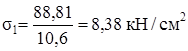 ,
, 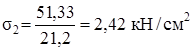 .
.
Напряжения меньше допускаемых (см. табл.2.1), прочность обеспечена.
На основании рассмотренных примеров можно отметить следующие особенности статически неопределимых конструкций, которыми они отличаются от статически определимых:
1. Распределение усилий между элементами статически неопределимых конструкций зависит от жёсткостей этих элементов. Если увеличить жёсткость какого- либо из них, то он примет на себя большее усилие.
2. В статически неопределимых конструкциях при изменении температуры её элементов по сравнению с температурой, при которой осуществлялась сборка конструкций, возникают усилия и напряжения.
3. В элементах статически неопределимых конструкций могут существовать усилия и напряжения при отсутствии внешней нагрузки. Эти усилия и напряжения, называемые начальными (монтажными), появляются при сборке конструкции. Начальные напряжения или создаются с определённой целью (например, затяжка болтов, прессовая посадка, предварительно напряжённый железобетон), или возникают вследствие неточного изготовления отдельных элементов конструкций.
4. В статически неопределимых конструкциях во всех элементах одновременно нельзя получить напряжения, равные допускаемым.
Для оценки прочностной надёжности конструкций необходимо изучить поведение материала в служебных условиях. В соответствии с принятой моделью материала (моделью сплошной среды) мы отказываемся от изучения внутренней микроструктуры материала (поведения кристаллической решетки, развития дислокаций и т.д.) и будем использовать феноменологический (описательный) подход. Такой подход означает, что, не вдаваясь в сущность внутренних процессов, явление (феномен) изучается по его внешним проявлениям. Феноменологический подход определяет необходимость экспериментального изучения механических свойств материалов.
Испытание материалов – это обширная специальная отрасль техники, использующая широкий спектр машин и приборов. Ограничимся лишь кратким описанием некоторых наиболее распространённых видов механических испытаний.
Испытание, как правило, заключается в изучении поведения образца в процессе деформирования его возрастающей нагрузкой до момента разрушения. Материалы при этом ведут себя по-разному: одни к моменту разрушения образца претерпевают значительные деформации, не исчезающие и после разрушения – это пластичные материалы (малоуглеродистая сталь, медь, латунь, алюминиевые и титановые сплавы), другие к моменту разрушения претерпевают весьма малые деформации – это хрупкие материалы (стекло, чугун, инструментальная сталь, некоторые пластмассы).
2.6.1. Испытание на растяжение малоуглеродистой (мягкой) стали
Основной вид испытания металлов, дающий наиболее полную информацию о механических свойствах, испытание на растяжение. Для него необходимо изготовить стандартные образцы, чаще всего их делают цилиндрическими (рис.2.15). В цилиндрических образцах должно быть выдержано соотношение между расчётной длиной образца ℓ0 и диаметром d0: у длинных образцов ℓ0 = 10d0 (рис.2.15,а), у коротких ℓ0 = 5d0 (рис.2.15,б).
а б
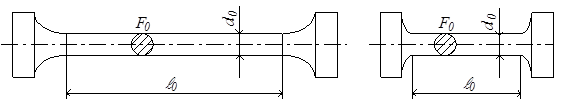
 2014-02-24
2014-02-24 1326
1326








