Условие прочности

Для решения вопроса о прочности, в соответствии с принятым методом расчёта на прочность по допускаемым на­пряжениям и условием прочности (1.4), запишем это условие применительно к растянутому (сжатому) стержню.

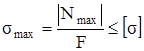, (2.3)

где |N_max| – максимальная по абсолютному значению продольная сила;

F – пло­щадь поперечного сечения стержня;

[σ] – допускаемое напряжение.

При реше­нии задач сопротивления материалов [σ] всегда задано. При расчётах машин или конструкций Нормы расчёта дают указания по поводу назначения или расчёта [σ]. Формула (2.3) применима для стержня из материала, имею­щего одинаковую прочность на растяжение и на сжатие (например, для стали). Но если материал по-разному сопротивляется растяжению и сжатию (напри­мер, чугун) для расчёта на прочность необходимо учитывать знак продольной силы и записывать два условия прочности

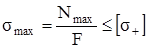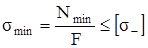, , (2.4)

где N_max – наибольшая (растягивающая) продольная сила;

N_min – наименьшая (сжимающая) продольная сила;

[σ₊] и [σ_-] – допускаемые напряжения на растяжение и на сжатие соответственно.

Значение N, входящее в условие прочности, определяется предварительно по эпюре N (рис.2.3.) или из расчёта статического равновесия конструкции.

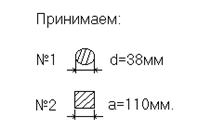
Рассмотрим пример. Необходимо определить размеры поперечного сечения стержней кронштейна, удерживающего нагрузку P = 100 кН (рис.2.6).

Стержень №1: стальной, круглый, [σ] = 160 МПа; стержень №2: деревянный, квадратный, [σ] = 12 МПа.

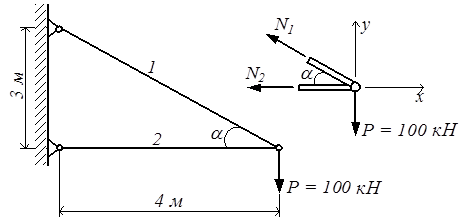
Рис.2.6

Сначала найдём усилия в стержнях. Для такой системы можно записать два уравнения статики:

∑ х = 0: – N₂ – N₁cos α = 0,

∑ y = 0: – P + N₁sin α = 0.

.

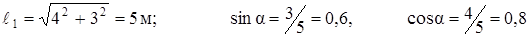Из уравнения ∑ y = 0 найдём .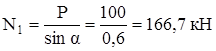

Из уравнения ∑ х = 0 найдём N₂ = – N₁cos α = – 166,7 ∙ 0,8 = – 133,3 кН.

Из условия прочности 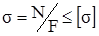найдём площади поперечного сечения стержней

, .

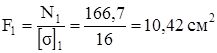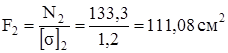При расчётах прочности величину допускаемого напряжения, заданную в МПа, перевели в кН/см²: 160 МПа = 16 кН/см² и 12 МПа = 1,2 кН/см². Теперь осталось определить размеры поперечных сечений.

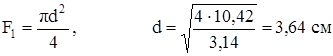F2 = a2, а = √111,08 = 10,54 см.