Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).
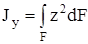 ,
, 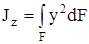 . (4.6)
. (4.6)
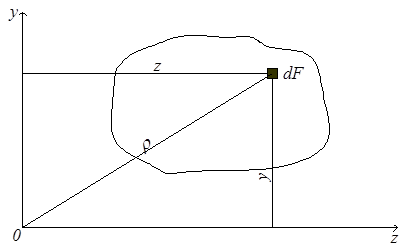
Рис.4.4
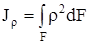 . (4.7)
. (4.7)
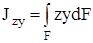 . (4.8)
. (4.8)
Если начало координат совпадает с полюсом, то ρ2 = z2 + y2, следовательно
Jρ = Jz + Jy. (4.9)
Размерность моментов инерции – единица длины в четвёртой степени (например, см4). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным
в зависимости от положения осей.
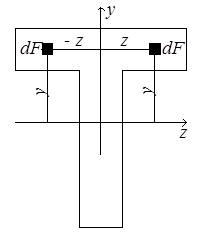 Рис.4.5
Рис.4.5
| Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.4.5) и их сумма по всей площади фигуры равна нулю. Главные оси, проходящие через центр тяжести, называются главными центральными осями. Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, Jzy = 0. |
а б
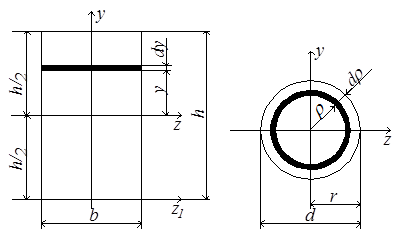
Рис.4.6
Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:
dF = bdy,
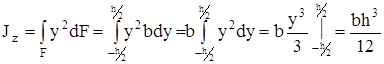 .
.
Очевидно, что для определения Jy надо поменять местами стороны прямоугольника.
Главные осевые моменты инерции прямоугольника
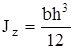 ,
, 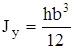 . (4.10)
. (4.10)
Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)
dF = 2πρdρ,
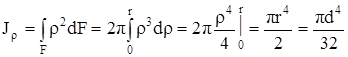 .
.
Полярный момент инерции круга
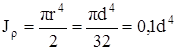 . (4.11)
. (4.11)
Осевой момент инерции круга легко найти из выражения (4.9), учитывая, что в силу симметрии Jz = Jy. Следовательно,
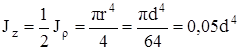 . (4.12)
. (4.12)
 2014-02-24
2014-02-24 2852
2852
