Рис.3.13
Аналогично получим выражения и для двух других главных удлинений. В результате
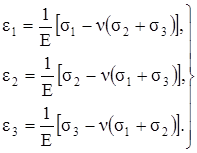 (3.25)
(3.25)
Формулы (3.25) носят название обобщённого закона Гука для изотропного тела. Заметим, что сжимающие напряжения подставляют в эти формулы со знаком минус. Из формул (3.25) легко можно получить закон Гука для плоского напряжённого состояния. Например, для случая σ2 = 0
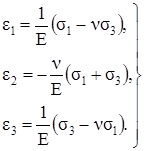 (3.26)
(3.26)
Подчеркнём, что равенство нулю напряжения σ2 не означает, что ε2 также равно нулю. Например, при растяжении пластинки в её плоскости по второй формуле (3.26) можно определить уменьшение толщины пластинки.
Выражения (3.25) справедливы не только для главных деформаций, но и для относительных линейных деформаций по любым трём взаимно перпендикулярным направлениям, поскольку при малых деформациях влияние сдвига от действия касательных напряжений на линейную деформацию представляет собой величину второго порядка малости. Иными словами, индексы «1», «2» и «3» могут быть заменены на индексы х, у и z.
3.5.2. Относительная объёмная деформация
Установим связь между относительным изменением объёма элементарного параллелепипеда и главными напряжениями. До деформации размеры сторон были dx, dy и dz (рис.3.14,а). После деформации эти размеры стали dx + ∆dx, dy + ∆dy и dz + ∆dz (рис.3.14,б).
а б
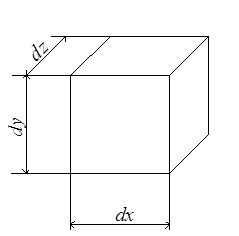
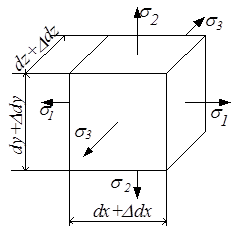
Рис.3.14
Начальный объём параллелепипеда V0 = dx∙dy∙dz. Объём после деформации V1 = (dx + ∆dx)(dy + ∆dy)(dz + ∆dz).
Найдём абсолютное изменение объёма параллелепипеда:
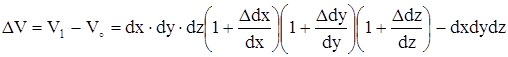 . (а)
. (а)
В скобках выражения (а) содержатся относительные удлинения
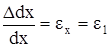 ,
, 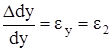 ,
, 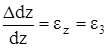 .
.
Произведя в выражении (а) перемножение величин, стоящих в скобках, получим
∆V = V0 ∙ (1 + ε1 + ε2 + ε3 + ε1ε2 + ε2ε3 + ε1ε3 + ε1ε2ε3) – V0.
Учитывая малость относительных деформаций, произведением их можно пренебречь. Тогда относительное изменение объёма
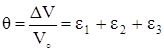 . (3.27)
. (3.27)
Выразив главные удлинения через главные напряжения при помощи формул обобщённого закона Гука (3.25), получим:
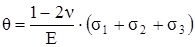 . (3.28)
. (3.28)
Формулу (3.28) перепишем в несколько ином виде, с учётом (3.22)
σ1 + σ2 + σ3 = 3σокт = 3σср.
Тогда
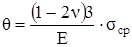 (3.29)
(3.29)
или
σср = K ∙ θ, (3.30)
где
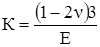 . (3.31)
. (3.31)
Величина К называется модулем объёмной деформации. Формула (3.30) представляет собой компактную, отличную от (3.25), формулу записи обобщённого закона Гука. Она удобна ещё и тем, что совпадает по структуре с законом Гука при линейном напряжённом состоянии (σ = Еε).
Из формулы (3.28) видно, что при деформации тела, материал которого имеет коэффициент Пуассона ν = 0,5 (например, резина или сталь в пластичном состоянии) объём тела не меняется. Материал ведёт себя как несжимаемая жидкость.
Из формулы (3.28) также следует, что коэффициент Пуассона не может быть больше 0,5. Действительно, при равномерном всестороннем сжатии (гидростатическом давлении) σср = – р. И если материал будет иметь ν > 0,5, тело увеличит свой объём, что невозможно. Опыты подтверждают это положение: в природе не существует материала с коэффициентом Пуассона, большим 0,5.
Как отмечалось выше (см. п. 2.8), в процессе упругой деформации в теле накапливается потенциальная энергия, равная работе внешних сил. При осевом растяжении (линейном напряжённом состоянии) удельная потенциальная энергия (т.е. энергия, приходящаяся на единицу объёма) определяется по формуле (2.37)
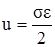 .
.
В общем случае объёмного напряженного состояния
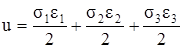 . (3.32)
. (3.32)
Подставив значения ε по формуле (3.25), получим
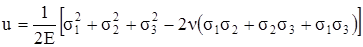 . (3.33)
. (3.33)
Экспериментальные исследования показали, что прочность материала зависит не только от величины компонентов напряжений, но и от характера напряжённого состояния. Так, большинство твёрдых тел противостоит без разрушения действию очень большого всестороннего давления – при этом изменяется объём бесконечно малого элемента. И наоборот, те же тела разрушаются при сравнительно невысоких напряжениях, если эти напряжения изменяют форму элемента. Поэтому полную потенциальную энергию упругой деформации, определяемую по формуле (3.33), представляют в виде суммы двух составляющих:
u = u0 + uф, (3.34)
где u0 – удельная потенциальная энергия изменения объёма, т.е. энергия, накапливаемая за счёт изменения объёма;
uф – удельная потенциальная энергия формоизменения, т.е. энергия, накапливаемая вследствие изменения формы элемента.
Для определения этих составляющих заданное напряжённое состояние представим в виде суммы двух напряжённых состояний (рис.3.15): изменяющего объём элементарного кубика (гидростатическое растяжение одинаковыми средними напряжениями) и изменяющего форму кубика.
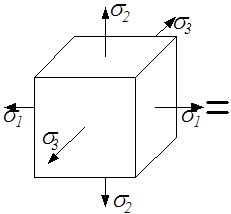
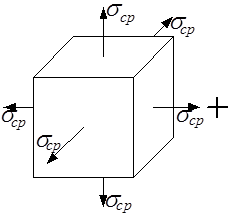
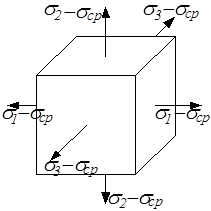
 2014-02-24
2014-02-24 1848
1848
