2014-02-24
439
Для описания условных законов распределения можно использовать различные характеристики подобно тому, как для одномерных распределений.
Наиболее важной характеристикой является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины 
при 
(
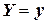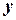– определённое возможное значение случайной величины 
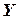) называется сумма произведений возможных значений на их условные вероятности:
.
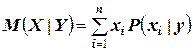Для непрерывных случайных величин:
,
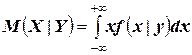где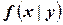 
– условная плотность распределения случайной величины при .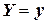
Аналогично, условным математическим ожиданием дискретной случайной величины 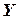при 
(
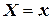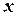– определённое возможное значение случайной величины) называется сумма произведений возможных значений 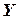на их условные вероятности:
.
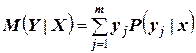Для непрерывных случайных величин:
,
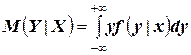где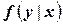 
– условная плотность распределения случайной величины 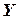при .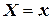
Аналогично вводятся условные дисперсии и условные моменты более высоких порядков (предлагаем это сделать самостоятельно).
|
|
|
