Коррелированность и зависимость случайных величин

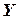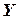Две случайные величины и называются коррелированными, если их корреляционный момент (или коэффициент корреляции) отличен от нуля; и называют некоррелированными величинами, если их корреляционный момент равен нулю.

Две коррелированные величины также и зависимы. Обратное утверждение не всегда имеет место, то есть если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равным нулю, но может и равняться нулю.

Заметим, что для нормально распределённых составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

Если 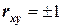, то и 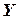связаны линейной зависимостью ,

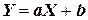Если 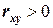, то говорят о положительной (или прямой) корреляции между и 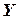, то есть с возрастанием одной случайной величины другая случайная величина также возрастает.

Если 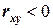, то говорят об отрицательной корреляции между и 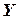, то есть с возрастанием одной случайной величины другая случайная величина убывает.