Законом распределения вероятностей системы случайных величин называется соответствие, устанавливающее связь между областями возможных значений данной системы случайных величин и вероятностями появления системы в этих областях.
Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы двух дискретных случайных величин. Пусть  и
и 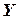 – дискретные случайные величины, возможные значения которых
– дискретные случайные величины, возможные значения которых 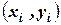 , где
, где 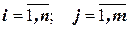 . Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей
. Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей 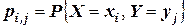 того, что случайная величина
того, что случайная величина  примет значение
примет значение 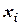 и одновременно с этим случайная величина
и одновременно с этим случайная величина 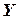 примет значение
примет значение 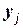 . Вероятности
. Вероятности 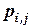 фиксируются в таблице
фиксируются в таблице
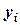
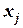
|
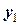
|
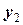
| ... |
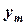
|
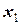
|
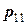
|
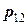
| ... |
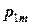
|
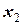
|
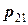
|
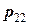
| ... |
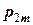
|
| . . . | . . . | . . . | . . . | . . . |
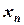
|
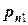
|
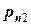
| ... |
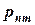
|
Такая таблица называется таблицей распределения вероятностей системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события 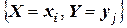 при
при 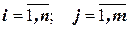 составляют полную группу несовместных событий, поэтому
составляют полную группу несовместных событий, поэтому
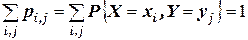 .
.
При этом:
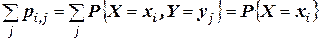 ;
;
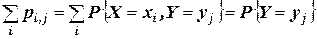 .
.
3. Функция распределения [19]
Функцией распределения вероятностей системы двух случайных величин называется функция 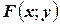 двух аргументов, равная вероятности совместного выполнения двух неравенств
двух аргументов, равная вероятности совместного выполнения двух неравенств 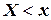 и
и 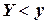 , то есть
, то есть 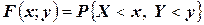 .
.
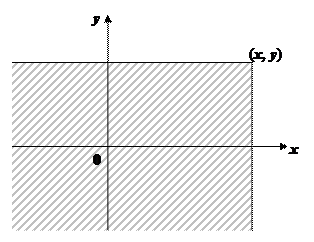
Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки 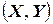 в левый нижний бесконечный квадрант с вершиной в точке
в левый нижний бесконечный квадрант с вершиной в точке 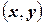 плоскости
плоскости 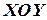 (см. рис.).
(см. рис.).
|
Сформулируем основные свойства функции распределения вероятностей системы двух случайных величин (без доказательства):
1. 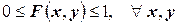
2.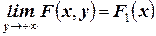 ;
; 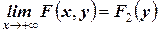 (или
(или 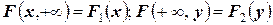 ).
).
3.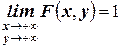 (или
(или 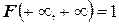 ).
).
4.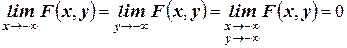 (
(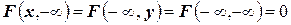 ).
).
5. Функция распределения является неубывающей функцией по каждому из своих аргументов, то есть:
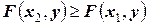 , если
, если 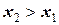 ;
;
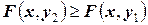 , если
, если 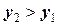 .
.

|
6. Вероятность попадания случайной точки 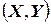 в произвольный прямоугольник со сторонами, параллельными координатным осям (см. рис.) вычисляется по формуле:
в произвольный прямоугольник со сторонами, параллельными координатным осям (см. рис.) вычисляется по формуле:
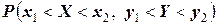 =
=
=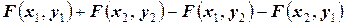 ,
,
где 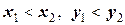 .
.
4. Плотность распределения вероятностей системы двух случайных величин [20]
Предположим, что функция распределения 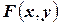 всюду непрерывна и дважды дифференцируема[21] (за исключением, быть может, конечного числа кривых). Тогда, смешанная частная производная функции
всюду непрерывна и дважды дифференцируема[21] (за исключением, быть может, конечного числа кривых). Тогда, смешанная частная производная функции 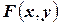
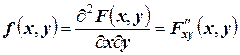 .
.
Функция 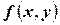 называется плотностью распределения (или, дифференциальной функцией распределения) системы непрерывных случайных величин
называется плотностью распределения (или, дифференциальной функцией распределения) системы непрерывных случайных величин 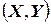 .
.
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
Зная плотность распределения 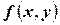 , можно определить вероятность попадания случайной точки
, можно определить вероятность попадания случайной точки 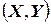 в произвольную область
в произвольную область 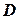 :
:
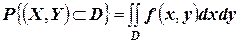 .
.
Используя последнюю формулу, выразим интегральную функцию 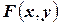 распределения вероятностей системы двух непрерывных случайных величин через плотность распределения
распределения вероятностей системы двух непрерывных случайных величин через плотность распределения 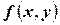 :
:
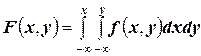 .
.
Рассмотрим некоторые свойства плотности распределения системы двух непрерывных случайных величин:
1. 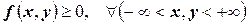 ;
;
2. 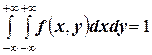 , если случайная величина
, если случайная величина 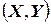 распределена на всей координатной плоскости (если же
распределена на всей координатной плоскости (если же 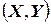 распределена в некоторой плоской области
распределена в некоторой плоской области 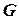 , то
, то 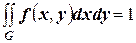 )
)
ПРИМЕР. Пусть плотность распределения системы двух случайных величин 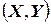 задана выражением:
задана выражением:
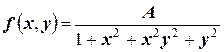 .
.
Найти параметр А. Определить функцию распределения 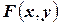 и вероятность попадания случайной точки
и вероятность попадания случайной точки 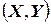 в прямоугольник
в прямоугольник 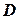 с вершинами:
с вершинами: 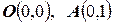 ,
, 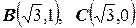 .
.
Решение. Использовав свойство 2 плотности распределения, найдём постоянную величину А:
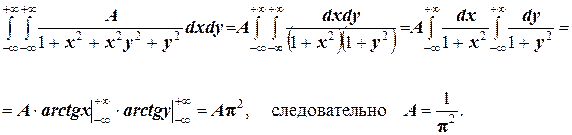
Определим теперь интегральную функцию распределения:
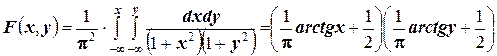 .
.
Таким образом, нетрудно теперь найти вероятность попадания случайной точки 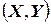 в заданный прямоугольник
в заданный прямоугольник 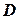 :
:
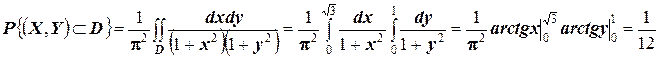 .
.
 2014-02-24
2014-02-24 1430
1430
