Коалиционные игры

В отличие от ранее рассмотренных классов задач, коалиционные игры решают задачу формирования оптимальных коалиций, выбора каждым из участников партнеров для сотрудничества.

Пусть имеется 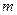участников:

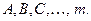
Рассмотрим возможные стратегии сотрудничества:

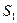– каждый из участников действует независимо от других;

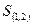– коалиция из двух участников, первого и второго;

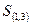– коалиция первого и третьего участников;

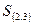– коалиция второго и третьего участников;

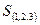– коалиция из трех участников.

Общее число возможных коалиций и, соответственно, стратегий равно 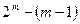. Для задания выигрышей при разных коалициях используется характеристическая функция. Например,

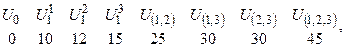
– выигрыш участников при стратегии

– если первый и второй участники вступят в коалицию, то их общий выигрыш составит 25 и т.д.

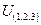– выигрыш трех участников, если они все вступят в коалицию.

Таким образом, чтобы описать коалиционную игру, необходимо задать характеристическую функцию.

Характеристическая функция должна обладать свойством супераддитивности. Для любой пары непересекающихся коалиций должно выполняться неравенство:

.

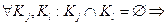
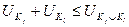Неравенство может быть и обратное – это означает, что в качестве выигрыша выступают затраты, убытки, и стоит задача выбора партнеров, чтобы уменьшить затраты, т.е. стоит задача минимизации целевой функции. Для этой постановки все рассматриваемые далее вопросы и процедуры тоже справедливы.

Если 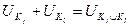, то такая игра несущественна, так как нет смысла вступать в коалиции.

Для решения игры необходимо составить матрицу выигрышей для каждого участника при разных стратегиях (коалициях) в следующем виде:

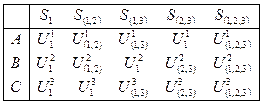
где 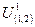– выигрыш участника в коалиции (1, 2), 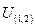– выигрыш участника в коалиции (1, 2) и т.д. При этом

.

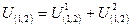Видим, что при определении выигрышей участников коалиций возникает проблема дележа.