Выигрыш игрока  , если
, если  принимает фиксированную чистую стратегию
принимает фиксированную чистую стратегию 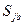 ,будет равен:
,будет равен:
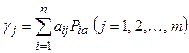 . (2.6)
. (2.6)
Найдем минимум из 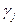 , обозначим его через
, обозначим его через 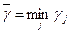 . Будем искать
. Будем искать 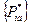 из условия
из условия 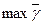 .
.
Все 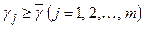 , так как
, так как 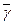 – минимальное. Поэтому (2.6) перепишем в виде неравенств:
– минимальное. Поэтому (2.6) перепишем в виде неравенств:
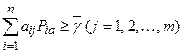 . (2.7)
. (2.7)
Для вероятностей 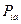 выполняется условие:
выполняется условие:
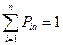 . (2.8)
. (2.8)
Нахождение 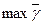 равносильно поиску
равносильно поиску 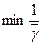 . Для удобства нахождения
. Для удобства нахождения 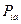 введем переменную
введем переменную 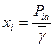 , тогда (2.7) перепишется в виде:
, тогда (2.7) перепишется в виде: 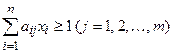 , а (2.8) – в виде
, а (2.8) – в виде 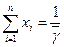 .
.
Определяем 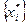 из условия, что
из условия, что 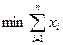 при ограничениях:
при ограничениях:
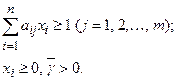
Для 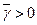 необходимо, чтобы все
необходимо, чтобы все 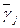 были положительные. Это обеспечивается, если все
были положительные. Это обеспечивается, если все 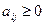 . Поэтому, если в матрице есть отрицательные элементы, увеличим все элементы
. Поэтому, если в матрице есть отрицательные элементы, увеличим все элементы 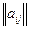 на
на 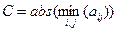 . При этом
. При этом 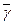 также увеличивается на
также увеличивается на 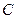 .
.
В результате решения поставленной задачи линейного программирования найдем 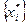 и значениецелевой функции
и значениецелевой функции 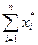 . После чего можем определить искомые
. После чего можем определить искомые 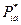 по формуле:
по формуле:
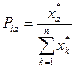 .
.
Выигрыш игрока  (цена игры) будет равен:
(цена игры) будет равен:
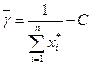 .
.
Алгоритм решения игры n x m для участника А
1. Переходим к положительным элементам матрицы: 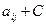 .
.
2. Решаем задачу линейного программирования:
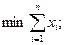
при ограничениях 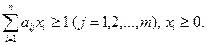
3. Находим вероятности: 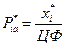 (
(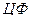 – значение целевой функции).
– значение целевой функции).
Выигрыш участника  определяется в соответствии с выражением:
определяется в соответствии с выражением: 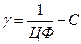 .
.
 2014-02-24
2014-02-24 380
380








