2014-02-24
1641
В биматричных играх задаются матрицы выигрышей для обоих участников:
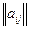– матрица 
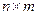выигрыша для игрока 
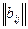– матрица 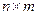выигрыша для игрока 
.
Необходимо найти оптимальные смешанные стратеги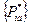и 
и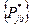 
.
2.4.1. Принципы решения биматричных игр
Пусть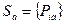 
–стратегия для игрока , а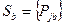 
–стратегия для игрока .
Определение 3 (приемлемая стратегия) Смешанная стратегия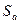 
является приемлемой для игрока , если для любой другой смешанной стратегии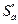 
и фиксированной смешанной стратегии 
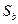полезность для игрока стратегии 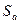больше, чем полезность стратегии 
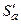. Таким образом, для любой смешанной стратегии 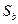можно определить приемлемую стратегию .
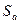Можно условно графически представить зависимость приемлемой стратегии 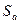как функцию от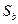, представленной на рис. 2.5.
Смешанная стратегия 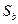игрока является приемлемой, если при любой другой смешанной стратегии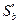 
и фиксированной смешанной стратегии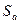выполняется:
.
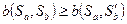Зависимость приемлемой стратегии 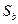от 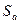также можно условно представить в виде функции 
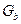(рис. 2.6).
Пересечение двух множеств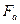 
и 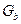дает решение биматричной игры (рис. 2.7):
|
|
|
Проиллюстрируем принцип решения биматричных игр на задаче размерности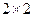 
.
2.4.2. Решение биматричных игр 2´2
В качестве исходных данных заданы две матрицы:
Смешанные стратегии 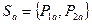для :
, для: 
.
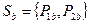Выигрыш участника равен:
.
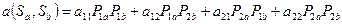С учетом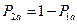 
и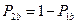 
:
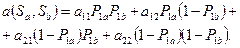
После упрощения получим:
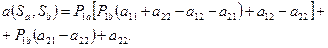
Так как в нашем случае смешанная стратегия 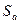определяется одной вероятностью 
, а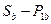 
, то условие приемлемой стратегии для 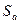запишется в виде:
.
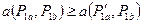Чистая стратегия 
будет приемлемой (лучшей), когда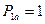 
или когда
.
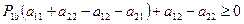Из данного неравенства можем сделать вывод, что чистая стратегия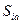 
–приемлемая, если 
:
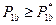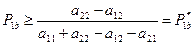
признаменателе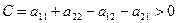
.
Если же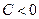 
, то тогда 
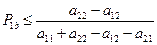,и –приемлемая при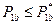 
.
Напротив, стратегия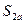 
приемлемапри 
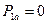, т.е.при условии, что
.
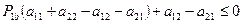Таким образом, при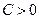 
стратегия 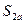приемлема, если
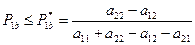, а при 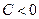– если .
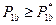На рис. 2.8 приведены зависимости пр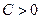и 
и.
|
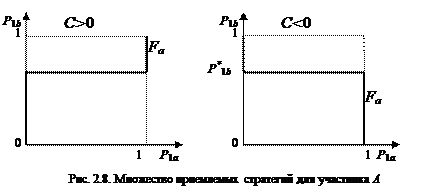
Для построения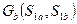 
запишем выражение для выигрыша участника :
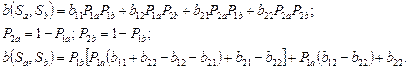
Чистая стратегия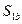 
– приемлемая 
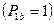, если
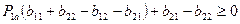
или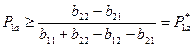 
,
при условии, что знаменатель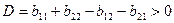 
.
Если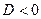 
, то чистая стратегия 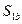приемлема при
.
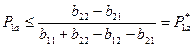На рис. 2.9 приведены зависимости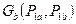 
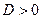при 
и.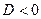
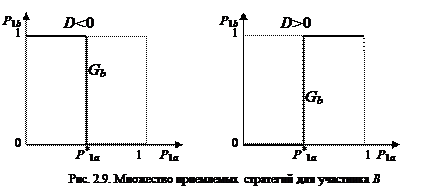
Решением биматричной игры будет пересечение 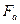и .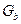
Возможны четыре варианта пересечения 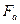и 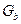(в зависимости от знаков 
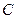и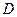
).
Первый вариант
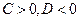. Решение единственное – 
.
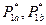Второй вариант
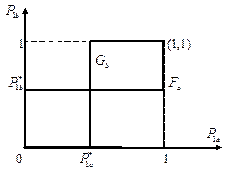
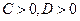.Решением будет 
, 
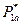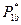, точки пересечения (1,1) и (0,0) – неустойчивы.
Третий вариант
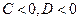. Решением будет 
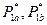. Точки (1, 0) и (0, 1) дают неустойчивые решения.
Четвертый вариант
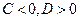. Решение единственное – , .
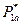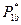Пример решения биматричной игры. Для каждого участника задана матрица выигрышей:
, 
.
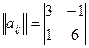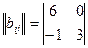Находим оптимальные смешанные стратегии:
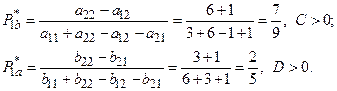
Рассчитываем выигрыши участников игры:
|
|
|
;
;
.
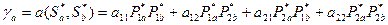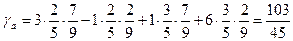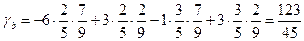Отметим, что принцип нахождения оптимальной смешанной стратегии для игрока А – минимизация выигрыша противника, и для участника В – тоже минимизация выигрыша противника. Этот принцип распространим для решения игр размерности n ´ m.
2.4.3. Решение биматричных игр n´m
Даны две матрицы выигрыше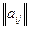й 
и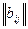 
размерности 
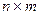. Необходимо найти оптимальные смешанные стратеги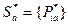и:
и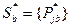 
.
Оптимальную смешанную стратегию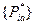 
находим из условия минимизации выигрыша противник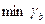а 
, а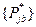 
– из условия минимизации выигрыша противника 
.
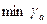Для нахождения 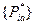ставимзадачу линейного программирования:
,
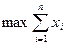при ограничениях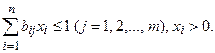 
На основе найденных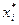 
вычисляем 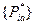(см. п. 2.3, решение матричных игр n ´ m).
Для нахождения 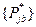ставим задачу линейного программирования: 
при ограничениях: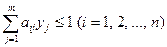
, 
.
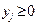На основе найденных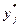 
вычисляем 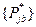(см. п. 2.3. решение матричных игр n´m).
Выигрыши участников определяются с использованием их матриц выигрышей:
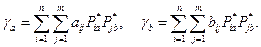
Следует сказать, что матричные (антагонистические) игры являются частным случаем биматричных игр, поэтому для их решения можно использовать принцип решения биматричных игр.
Следует также отметить, что принцип решения биматричных игр может использоваться для решения игр с тремя и более участниками. Чтобы это продемонстрировать, рассмотрим решение диадических игр с тремя участниками.
