Перейдем к матрице 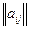 с неотрицательными элементами так же как и при решении для участника А. Через
с неотрицательными элементами так же как и при решении для участника А. Через 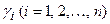 обозначим проигрыш игрока
обозначим проигрыш игрока  при фиксированной стратегии игрока
при фиксированной стратегии игрока  :
:
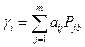 .
.
Для вероятностей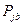 выполняется условие:
выполняется условие: 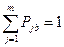 .
.
Введем обозначение 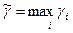 . Задача минимизации
. Задача минимизации 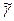 эквивалентна поиску
эквивалентна поиску 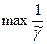 .Произведем замену переменных:
.Произведем замену переменных:
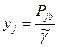 .
.
Получаем задачу линейного программирования:
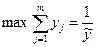
при ограничениях: 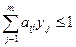 (при
(при 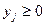 ).
).
Решив задачу линейного программирования, получим 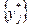 и значение целевой функции (
и значение целевой функции (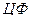 ). Цена игры –
). Цена игры – 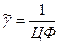 , а искомые вероятности –
, а искомые вероятности – 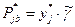 .
.
Алгоритм решения игры n x m для участника В
1. Переходим к положительным элементам платежной матрицы:
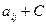 .
.
2. Решаем задачу линейного программирования:
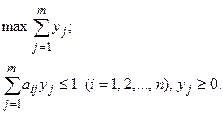
3. Интерпретируем результаты:
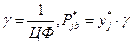 .
.
4. Корректируем 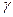 :
:
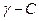 .
.
Вернемся к теореме о минимаксе (см. п. 2.3).
Теорема о минимаксе. В матричной игре без седловой точки 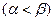 существует точка равновесия такая, что
существует точка равновесия такая, что 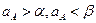 , и оптимальные решения для участников находятся из условий:
, и оптимальные решения для участников находятся из условий:
для  –
–  из условия
из условия 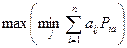 ,
,
для  –
– 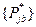 из условия
из условия 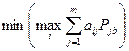 ,
,
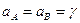 – цена игры.
– цена игры.
Доказательство.
В соответствии с рассмотренным алгоритмом существует решение для участника А 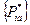 ,определяемоеиз условия:
,определяемоеиз условия:
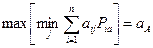 ;
;
и существует решение для участника В 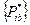 ,определяемоеиз условия:
,определяемоеиз условия:
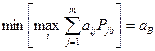 .
.
Из теоремы о прямой и двойственной задачах линейного программирования следует, что 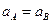 .
.
 2014-02-24
2014-02-24 363
363








