Введение в теорию полей. Комплексные числа

Эта часть конспекта имеет двоякую цель. С одной стороны, она покажет вам новый подход к построению поля комплексных чисел C, а с другой – подготовит почву для атаки (в далёком будущем, так что храните этот конспект!) на проблему разрешимости уравнений в радикалах и построений циркулем и линейкой.

Пусть F – подполе поля Е, FÌE. В этом случае Е называют расширением поля F.

Во-первых, а много ли для этого надо?

Упражнение 1. Достаточно ли для этого, чтобы подмножество FÌE было просто замкнутым относительно операций сложения и умножения?

А во-вторых, если F – подполе поля Е, а А={a,b,g,..} – множество каких-то не входящих в F элементов Е, то

Упражнение 2. как выглядит минимальное поле, содержащее подполе F и все эти элементы множества А? Какие элементы оно обязано содержать? Оно будет, разумеется, пересечением всех подполей Е, содержащих как F, так и А. Начните с самого простого случая, когда всё А состоит из одного элемента, А={a}. Такое расширение поля F обозначим как F(a). FÌF(a)ÌE.

Def. Соответственно, расширение подполя F, полученное с помощью А={a,b,g,..} обозначается F(a,b,g,..) и называется полем, полученным присоединением элементов a,b,g,..к полю F или полем, порождённым элементами a,b,g,..над F.

Если в Е рассматривать только сложение, а в FÌE – обе операции, сложение и умножение, то пара (F,E) представляет собой векторное пространство:
Е – абелеву группу, а F – действующее на неё поле. Векторами будут выступать элементы Е, а коэффициентами – элементы F. Именно такое рассмотрение и оказалось наиболее плодотворным – мы можем применить развитую теорию векторных пространств.
Например, Е может иметь конечную размерность dim_FE. В этом случае говорят, что

Def. Е – конечное расширение над F, размерность Е над F называют степенью Е над F и обозначают как (E/F).

Упражнение 3.

Пусть FÌEÌG – поля. Тогда (G/F)=(G/E)×(E/F)

* Упражнение 4.

Пусть fÎF[X], degf=n; f(x) – неприводимый многочлен над полем F.
Тогда не существует двух многочленов g, hÎF[X], таких, что degg<n, degh<n и g×h M f.

(Of course, prove from the opposite. If there are such pairs (g,h) which satisfy the assumption, chose from all these pairs the one, where g has the least degree. So done, there exist kÎF[X], such, that k(x)f(x)=g(x)h(x). Take advantage of the Euclid algorithm for polynoms: f=q×g+r, degr<degg. Time this identity by h and find out that (r,h) also satisfies the assumption – it contradicts with the choice of g)

Def. Пусть FÌE, aÎE. Если существуют многочлены с коэффициентами из F, такие, что a является их корнем, то элемент a называется алгебраическим над F.

Упражнение 5. Почему все элементы поля F являются алгебраическими над F?

Упражнение 6. Является ли 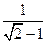алгебраическим над Q в Q(Ö2)?

Пусть aÎE – алгебраический над F. Пусть fÎF[X] – многочлен минимальной степени из всех многочленов, для которых a является корнем. Пусть ещё при этом старший коэффициент многочлена f равен единице. Этого всегда можно добиться умножением на обратный элемент к старшему коэффициенту в поле F всех коэффициентов многочлена f. Многочлен со старшим коэффициентом 1 называется приведённым. Тогда

Упражнение 7.

· Такой многочлен f однозначно определён;

· В кольце многочленов F[X] многочлен f порождает главный идеал (f)=f×F[X], в котором лежат все многочлены, для которых a является корнем;

· многочлен f неприводим.

(again, let g(a)=0 and use the Euclid algorithm)

Таким образом, имеет место отображение множества всех алгебраических элементов поля Е во множество F[X] многочленов с коэффициентами из F. Это отображение a®f_a может быть не инъективно и не сюръективно: в QÌ Q(Ö2) (Ö2) и -(Ö2) отобразятся в х²-2, в то же время х²-3 вообще не имеет прообраза в Q(Ö2). Тем не менее, каждому алгебраическому элементу a поставлен в соответствие некоторый, однозначно определённый, неприводимый f_a.

Фиксируем элемент a и пусть a®f_a и degf_a=n. Пусть F_n-1[X]Ì F[X] - векторное пространство всех многочленов степени не выше n-1 с коэффициентами из F, а Е_aÌЕ –множество всех элементов ӨÎЕ, представимых в виде Ө=g(a)=c₀+c₁a+c₂a²+…+c_n-1a^{n-1, g}ÎЕ_a.

Упражнение 8.

Каждому такому Ө многочлен g соответствует однозначно, т.е. все его коэффициенты однозначно определяются; никакой другой многочлен из F_n-1[X] представлять элемент Ө не может. Т.е., не может быть того, что помимо Ө=g(a) ещё и Ө=h(a).

Очевидно, что Е_a – векторное подпространство Е над F. Почему? Какова его размерность? Менее очевидно (то, что вам предлагается доказать), что

Упражнение 9.

Е_a замкнуто и относительно умножения! (hint: again, use Euclid algorithm and definition of f_a)

Теперь отвлечёмся от элемента a.

Пусть дан неприводимый (но приведённый!) многочлен f(X)=Xⁿ+a_n-1X^n-1+…+a₀
с коэффициентами a_iÎF. Рассмотрим n-мерное ВП E_f (над F, разумеется) всех многочленов степени £n-1. Помимо обычного сложения, введём в нём и «необычное» умножение, а именно: произведением двух многочленов будем называть остаток от деления их обычного произведения на многочлен f(X).

Если новое произведение обозначать символом «´», а старое – символом «×», то g(X)´h(X)=g(X)×h(X)(mod f(X)).

Упражнение 10.

a) Пусть F=Q, f(X)=X³-3.
Найдите произведение g(X)´h(X) для g(X)=2Х²-1 и h(X)=Х²-Х-1.

b) Пусть F=R, f(X)=X²+1.
Найдите произведение g(X)´h(X) для g(X)=2Х-1 и h(X)=Х+2.

Упражнение 11.

Проверьте, что относительно сложения и умножения «´»E_f является кольцом (делается точно так же, как и Z/mZ – с использованием алгоритма Евклида).

Упражнение 12.

Вычислите значение Хⁿ в E_f. Убедитесь в том, что E_f содержит F в качестве подполя. И, наконец, проверьте, что…многочлен Х – элемент E_f – является решением уравнения f(X)=0!

Прозорливы оказались те из вас, кто уже заподозрил, что это E_f является, не просто векторным пространством и одновременно кольцом (такие объекты называются алгебрами), а самым что ни на есть настоящим полем. Подозрения эти основывались на воспоминаниях о том, что Z/mZ оказывалась полем, когда m – простое, а в случае многочленов эту роль выполняют неприводимые. Для проверки того, что E_f является полем достаточно проверить, что у каждого ненулевого элемента E_f имеется обратный элемент.

Прежде чем делать это в общем случае, потренируйтесь: найдите обратные элементы к многочленам g(X)=Х²-Х и g(X)=2Х+1 в E_f из пунктов а) и b) соответственно упражнения 10. Вы найдёте коэффициенты искомых многочленов, решая линейные уравнения. Выручают при этом старшие степени – как раз они-то и обеспечивают разрешимость. В общем случае разрешимость соответствующей системы уравнений вытекает из того факта, что соответствующая ей однородная система имеет только тривиальное решение – а это, в свою очередь, следует из упражнения 4.

Итак, пусть дан g(X)=b₀+b₁X+b₂X²+..+b_n-1X^n-1.

Упражнение 13*.

Докажите, что найдётся h(X)= c₀+c₁X+c₂X²+..+c_n-1X^n-1 такой, что h(X) ´ g(X)=1.

Упражнение 14.

Пусть aÎE – алгебраический над F и f_a – тот самый многочлен, который ему соответствует по теореме 7; a®f_a. Докажите, что Е_a изоморфно полю E_f и, тем самым, само является полем.

Из упражнений 12 и 14 вытекает теорема Кронекера:

Упражнение 15.

Для произвольного многочлена f(x) над полем F существует расширение Е поля F в котором f(x) имеет корень.

Между прочим, для тех, кто не забывает прошлые конспекты: то, что E_f окажется полем, было ясно уже хотя бы потому, что F[X] – кольцо главных идеалов (см. Rings, ex #31). При этом идеал (f) прост в силу неприводимости f. В к.г.и. же все простые идеалы – максимальные, а факторкольцо по максимальному идеалу – поле (см. Rings, ex #36).

То, что мы обсуждали до сих пор, относится к любым полям и любым неприводимым над ними многочленам. Эти общие соображения нам понадобятся в дальнейшем, а пока вернёмся к нашему конкретному примеру: расширению уже построенного в предыдущем конспекте поля вещественных чисел R с помощью неприводимого над этим полем многочлена f(X)=X²+1. В этом поле E_f, полученном факторизацией кольца всех многочленов над R по идеалу, порождённому многочленом f(X)=X²+1, сам многочлен X²+1, естественно, - нулевой (вместе со всем идеалом кратных ему многочленов). Само поле Е=R[X]/(X²+1) имеет базис {1,X} как ВП над R. Таким образом, оно изоморфно (как ВП) плоскости R². Умножение в Е позволяет определить умножение векторов на плоскости.

Упражнение 16.

Пусть (a,b) и (с,d) вектора, соответствующие многочленам a+bX и c+dX. Каковы будут координаты вектора – произведения этих двух векторов?

Теперь вспомним, как мы вводили комплексные числа (вернее, тогда это были рационально-комплексные числа, поскольку в нашем распоряжении ещё не было поля вещественных чисел R). Тем более, что этот важный материал не был отражён в конспектах.

Мы искали решение уравнения X²+1=0. Было очевидно, что среди «старых» чисел на числовой прямой его нам не найти. Требовалось изменить сам взгляд на природу чисел. Но среди новых объектов надо было найти, всё-таки, образы старых чисел, которые бы однозначно им соответствовали, и операции над ними происходили бы по тем же правилам. Такие образы мы нашли в виде операции гомотетии на (векторной!) плоскости Q². Каждому старому числу a мы поставили операцию растяжения векторов в a раз. В любом базисе такому линейному преобразованию соответствует матрица 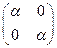. Во множестве всех линейных операторов, действующих на векторной плоскости, есть и другие операторы, помимо гомотетии – что и позволяет расширить понятие числа и поискать решение уравнения именно там. Кроме того, в пространстве операторов уже имеются операции сложения и умножения (последовательного выполнения, или композиции) которые обладают всеми необходимыми свойствами кроме двух: не каждый оператор имеет обратный относительно умножения и умножение, вообще говоря, не коммутативно. Роль нуля играет отображение «всех – в ноль!», имеющее матрицу 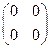, а роль нейтрального по умножению, единицы, (единичной матрицы) играет тождественное отображение id «всем оставаться на местах!», имеющее матрицу Е= 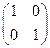. Но отображение a®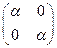является изоморфизмом, т.е. «старые числа» вкладываются изоморфно в кольцо линейных операторов. В этом кольце роль «-1» играет, естественно, гомотетия с коэффициентом -1, отражающая каждый вектор в обратный ему относительно операции сложения и имеющая матрицу матрица –Е=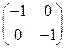в любом базисе. Уравнение же X²+Е=0 в линейных операторах на плоскости вы легко решили: его решением служит оператор поворота на 90°. Его матрицей в стандартном базисе (т.е., в базисе e ₁=(1,0); e ₂=(0,1)) служит матрица J=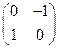. Если вы не уверены, как умножать матрицу на число, можно сложить матрицу саму с собой – это будет её умножением на 2. При этом все компоненты матрицы удвоятся. Стало быть, при умножении матрицы на число все её компоненты умножаются на это число. Точно такой же эффект получится (проверьте), если вы её умножите (неважно, справа или слева) на диагональную матрицу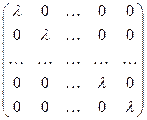. Эту матрицу можно записать, как lЕ. Если мы строим новые числа, то они должны быть замкнуты относительно операций сложения и умножения. Мы имеем уже все диагональные матрицы и матрицу J. Стало быть, мы должны иметь и все их произведения, т.е., матрицы вида bJ=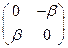. Всевозможные суммы этих матриц с диагональными дают матрицы вида lЕ+bJ=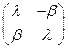. А далее нам просто повезло: оказалось, что матрицы этого вида не только сохраняют свой вид при сложении (что очевидно), но и при умножении. При этом оказалось, что умножение таких матриц не зависит от порядка сомножителей, хотя, как мы знаем, вообще говоря, умножение матриц не коммутативно (при этом примеры, это демонстрирующие, весьма просты). Мало того, оказалось, что и обратные матрицы существуют (и имеют тот же вид!) ко всем таким матрицам, кроме нулевой. Таким образом, мы построили поле C, подполе в кольце квадратных матриц второго порядка. Оно же является и векторным двумерным пространством, т.е., алгеброй (раньше - над Q, теперь - над R) с базисом (Е, J). Изоморфизм Е®(1,0); J®(0,1) позволяет перенести умножение из C на R².

Упражнение 17.

Чему будет равно произведение векторов е =(a,b) и f =(с,d) при этом изоморфизме?

Сравнение с результатом предыдущего упражнения показывает, что хотя и способ построения алгебры комплексных чисел и их природа (многочлены, матрицы, вектора на плоскости) были различны, все они оказались изоморфными, привели к двумерной алгебре над полем R, в которой умножение определяется по формуле, которую вы только что получили. Именно так – по этой формуле, без объяснения, откуда она такая и почему именно такая взялась, обычно и вводят понятие комплексного числа в школе. Вы же получили оба способа – с помощью обращения к линейным операторам на плоскости и с помощью факторизации алгебры многочленов по многочлену X²+1 и убедились в том, что привели они к одному и тому же результату (с точностью до изоморфизма). Это – различные модели одной и той же комплексной плоскости С.

Вектор (1,0) – это просто единица поля вещественных чисел R и её можно так и обозначить, (1,0)=1. Вектор (0,1) обозначается буквой i и называется мнимой единицей. Тогда произведение векторов е =(a,b)=a×1+b×i и f =(с,d)=c×1+d×i производится по правилу умножения многочленов – раскрытия скобок в выражении (a+bi)×(c+di) c учётом того, что i²=-1.