Базис- мерного пространства

Пусть задана система 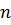- мерных векторов 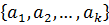из пространства .

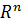Вектор вида 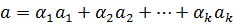, для некоторых чисел 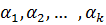называется линейной комбинацией этих векторов.

Пример 30. Для трехмерных векторов 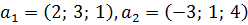пространства 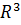, вектор 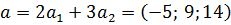является линейной комбинацией векторов 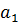и .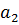

Система 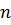- векторов 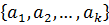называется линейно независимой, если из того, что 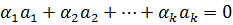, всегда следует

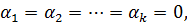
в противном случае система называется линейно зависимой.

Линейную зависимость 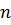– векторов можно выразить следующим образом:

Пусть 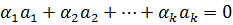и векторы 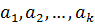являются линейно зависимыми, тогда, по крайней мере, одно из чисел 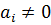(например, 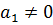) и 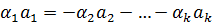, 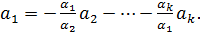Вектор 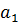является линейной комбинацией остальных векторов. Таким образом, система

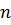– векторов линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных.

Система векторов 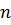- мерного пространства зависима тогда и только тогда, когда ранг матрицы, строки которой являются векторами системы меньше их количества. Если же ранг матрицы в точности равен количеству этих векторов, то они являются линейно независимыми.

Рангом системы 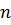– векторов называется максимальное количество линейно независимых векторов этой системы.

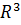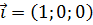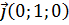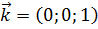Пример 31. В пространстве единичные векторы , и являются линейно независимыми.

Базисом 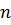- мерного векторного пространства 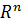называется любая линейно - независимая система векторов, через которые можно выразить любой вектор пространства. Базисов в пространстве может быть бесконечное множество. Количество векторов в базисе пространства называется его размерностью.

Теорема 5. Базис 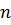- мерного пространства 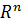состоит из 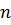векторов.

Доказательство. Покажем линейную независимость системы векторов

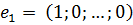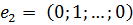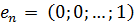, , …, . Пусть

.

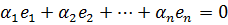Запишем это равенство в координатной форме

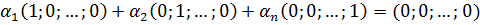, или

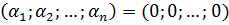, отсюда 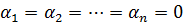, т. е. векторы

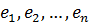– линейно независимы.

Для произвольного вектора 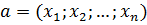, очевидно равенство

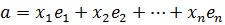. Таким образом, векторы 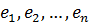образуют базис пространства.

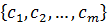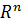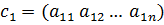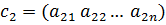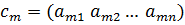Предположим, что существует другой базис , пространства , где , ,…, и 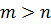, т. е. число векторов которого больше n. Тогда выполняется равенство 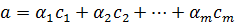, что равносильно системе

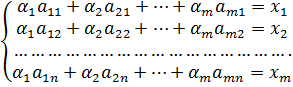
Число уравнений системы меньше, чем число неизвестных, поэтому ранг матрицы системы ограниченной не может быть больше, чем n, следовательно, система векторов линейно зависима и не может образовывать базис. Теорема доказана.

Координаты векторов.

Если в пространстве 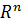выбран некоторый базис 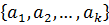, то для произвольного вектора 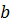справедливо представление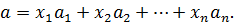

Числа 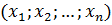называются координатами вектора 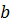в базисе 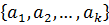. В различных базисах пространства 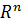один и тот же вектор будет иметь различные координаты.