Векторные пространства.
Арифметическим 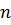 - вектором называют упорядоченный набор из
- вектором называют упорядоченный набор из 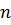 действительных чисел. Обозначается как
действительных чисел. Обозначается как 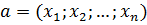 , где
, где 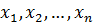 – действительные числа. Вектор
– действительные числа. Вектор 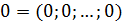 – называется нулевым
– называется нулевым 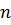 - вектором.
- вектором.
Пусть 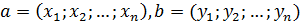 , λ – некоторое число Определим сумму
, λ – некоторое число Определим сумму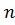 – векторов и произведение
– векторов и произведение 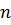 – вектора на число λ следующим образом:
– вектора на число λ следующим образом:
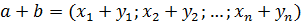 ,
,
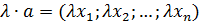 .
.
Множество всех 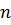 - мерных векторов называется арифметическим векторным пространством и обозначается -
- мерных векторов называется арифметическим векторным пространством и обозначается - 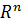 . Так в качестве
. Так в качестве 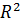 можно рассматривать множество всех векторов на плоскости,
можно рассматривать множество всех векторов на плоскости, 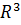 – множество всех векторов в пространстве.
– множество всех векторов в пространстве.
Аксиомы векторного пространства.
Для любых векторов 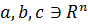 и чисел
и чисел 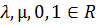 выполняются следующие свойства:
выполняются следующие свойства:
1) 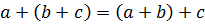 (ассоциативность суммы векторов);
(ассоциативность суммы векторов);
2) 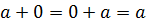 (наличие нейтрального элемента для суммы векторов);
(наличие нейтрального элемента для суммы векторов);
3) 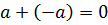 (наличие противоположного вектора);
(наличие противоположного вектора);
4) 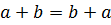 (коммутативность);
(коммутативность);
5) 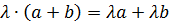 (дистрибутивность умножения на сумму векторов);
(дистрибутивность умножения на сумму векторов);
6) 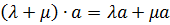 (дистрибутивность произведения суммы чисел на вектор);
(дистрибутивность произведения суммы чисел на вектор);
7) 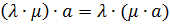 (ассоциативность умножения произведения чисел на вектор);
(ассоциативность умножения произведения чисел на вектор);
8) 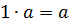 (существование нейтрального элемента при умножении чисел на вектор).
(существование нейтрального элемента при умножении чисел на вектор).
Свойства 1 – 8 называются аксиомами 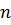 – векторного пространства.
– векторного пространства.
В общем случае, множество для которого выполняются аксиомы 1 – 8 называется линейным векторным пространством.
Скалярным произведением 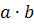 двух
двух 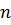 – векторов
– векторов 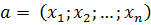 и
и 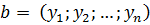 называется число, равное
называется число, равное
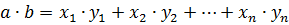 .
.
На основании скалярного произведения вводится длина вектора как квадратный корень из его скалярного квадрата, т. е. если 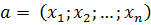 , то
, то
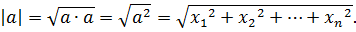
Введенная таким образом длина 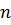 – вектора обладает всеми свойствами длины векторов плоскости и пространства.
– вектора обладает всеми свойствами длины векторов плоскости и пространства.
Свойства длины 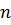 – вектора.
– вектора.
1. 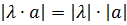 , для любого
, для любого 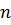 – вектора
– вектора 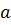 и числа
и числа 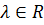 .
.
2. 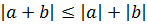 , для любых
, для любых 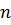 – векторов
– векторов 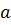 и
и 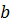 (неравенство треугольника).
(неравенство треугольника).
Угол 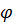 между векторами
между векторами 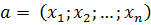 и
и 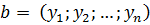 определяется равенством
определяется равенством 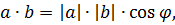 откуда
откуда
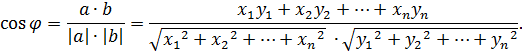
 2014-02-09
2014-02-09 402
402







