Линейные операторы

В пространстве 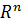можно определить преобразования, которые сохраняют линейные операции.

Отображение 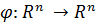векторного пространства называется линейным оператором, если для любых векторов 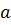, 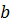и для любого числа 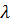выполняются условия:

1) ;

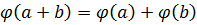2) .

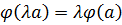Теорема 6. Всякий линейный оператор однозначно определяется некоторой матрицей .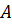

Доказательство. Пусть задан линейный оператор 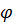и некоторый базис 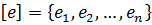. Выразим векторы 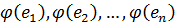через векторы базиса .

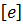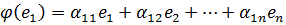
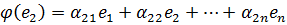
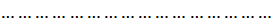
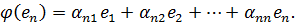
Обозначим

,

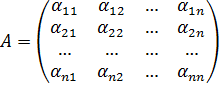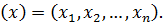
Тогда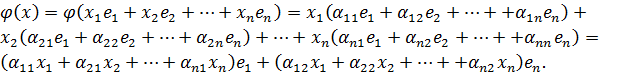

Отсюда .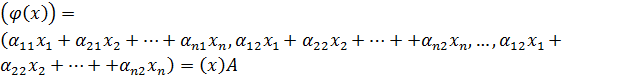

Таким образом, действие оператора 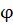на произвольный вектор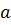

полностью определяется умножением координатной строки вектора на матрицу 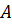. Теорема доказана.