Собственным вектором линейного преобразования 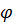 (или соответствующей матрицы
(или соответствующей матрицы 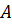 ) называется такой вектор
) называется такой вектор 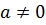 , что
, что 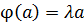 . Число
. Число 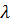 называется собственным значением оператора
называется собственным значением оператора 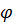 для вектора
для вектора 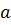 . После линейного преобразования
. После линейного преобразования 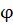 векторы
векторы 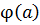 и
и 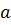 являются коллинеарными.
являются коллинеарными.
Пусть 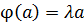 для некоторого собственного вектора
для некоторого собственного вектора 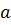 и собственного значения
и собственного значения 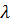 . Тогда
. Тогда 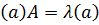 ,
, 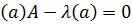 или
или 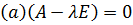 . Так как
. Так как 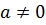 , то
, то 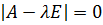 . Последнее уравнение называется характеристическим.
. Последнее уравнение называется характеристическим.
Таким образом, собственные значения являются корнями характеристического уравнения.
Пример 32. Найти все собственные значения и собственные векторы линейного преобразования 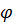 пространства
пространства 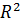 имеющего матрицу
имеющего матрицу
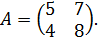
Решение. Составим характеристическое уравнение 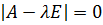 .
.
В нашем случае
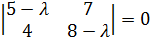 .
.
Откуда 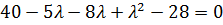 ,
, 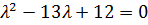 и
и 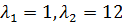 .
.
Случай 1. 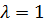 . Тогда для собственного вектора
. Тогда для собственного вектора 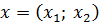 получим матричное равенство
получим матричное равенство 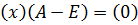 , или
, или
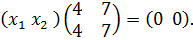
Перемножая матрицы слева и сравнивая элементы, получим систему
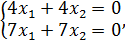
которая равносильна уравнению с двумя неизвестными 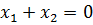 .
.
Положим 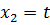 , получим
, получим 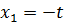 . Таким образом, все собственные векторы, соответствующие собственному значению
. Таким образом, все собственные векторы, соответствующие собственному значению 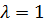 , имеют вид
, имеют вид
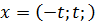 , где
, где 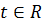 .
.
Случай 2. 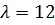 . Тогда для собственного вектора
. Тогда для собственного вектора 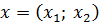 получим матричное равенство
получим матричное равенство 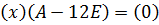 , или
, или
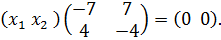
Перемножая матрицы слева и сравнивая элементы, получим систему
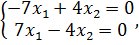
которая равносильна уравнению с двумя неизвестными 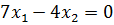 .
.
Положим 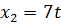 , получим
, получим 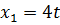 . Таким образом, все собственные векторы, соответствующие собственному значению
. Таким образом, все собственные векторы, соответствующие собственному значению 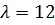 , имеют вид
, имеют вид
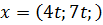 , где
, где 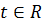 .
.
Пример 33. Найти все собственные значения и собственные векторы линейного преобразования 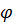 пространства
пространства 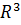 имеющего матрицу
имеющего матрицу
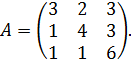
Решение. Составим характеристическое уравнение 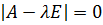 .
.
В нашем случае
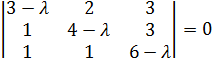 .
.
Разложим определитель по элементам первого столбца
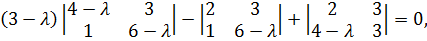
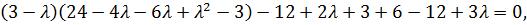
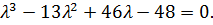
Подстановкой убеждаемся, что 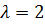 является корнем уравнения. Разделив левую часть уравнения на
является корнем уравнения. Разделив левую часть уравнения на 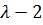 , получим разложение
, получим разложение
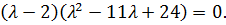
Откуда 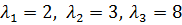 . Найдем собственные векторы для каждого их найденных собственных значений.
. Найдем собственные векторы для каждого их найденных собственных значений.
Случай 1. 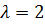 . Тогда для собственного вектора
. Тогда для собственного вектора 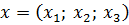 получаем матричное равенство
получаем матричное равенство 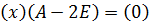 , или
, или
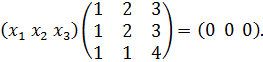
Перемножая матрицы слева и сравнивая элементы, получим систему
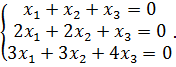
Решая систему методом Гаусса, приведем расширенную матрицу к ступенчатому виду
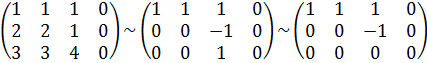 .
.
Получаем систему
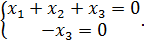
Положим 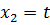 , получим
, получим 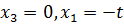 . Таким образом, все собственные векторы, соответствующие собственному значению
. Таким образом, все собственные векторы, соответствующие собственному значению 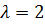 , имеют вид
, имеют вид
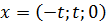 , где
, где 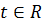 .
.
Случай 2. 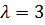 . Тогда для собственного вектора
. Тогда для собственного вектора 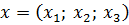 получаем матричное равенство
получаем матричное равенство 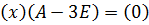 , или
, или
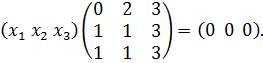
Перемножая матрицы слева и сравнивая элементы, получим систему
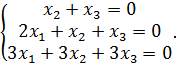
Решая систему методом Гаусса, приведем расширенную матрицу к ступенчатому виду, предварительно сократив третье уравнение на 3 и поменяв его местами с первым
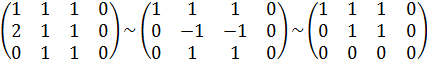 .
.
Получаем систему
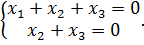
Положим 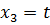 , получим
, получим 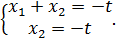
Отсюда 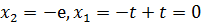 . Таким образом, все собственные векторы, соответствующие собственному значению
. Таким образом, все собственные векторы, соответствующие собственному значению 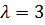 , имеют вид
, имеют вид
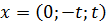 , где
, где 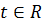 .
.
Случай 3. 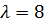 . Тогда для собственного вектора
. Тогда для собственного вектора 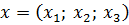 получаем матричное равенство
получаем матричное равенство 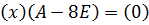 , или
, или
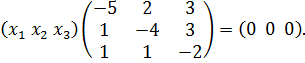
Перемножая матрицы слева и сравнивая элементы, получим систему
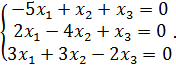
Решая систему методом Гаусса, приведем расширенную матрицу к ступенчатому виду
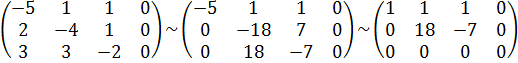 .
.
Получаем систему
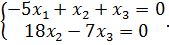
Положим 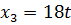 , получим
, получим 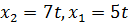 . Таким образом, все собственные векторы, соответствующие собственному значению
. Таким образом, все собственные векторы, соответствующие собственному значению 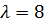 , имеют вид
, имеют вид 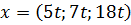 , где
, где 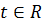 .
.
 2014-02-09
2014-02-09 375
375








