2014-02-24
606
Чтобы полнее выявить характер протекания переходного процесса рассмотрим режим приема и сброса нагрузки. Этот процесс происходит при по шаговой работе и в цепи якоря нет никаких дополнительных сопротивлений,
при этом процесс может носить колебательный характер.
запишем в следующем виде:
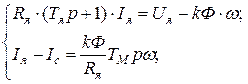
Для данной системы изобразим структурную схему:
С помощью этой схемы получим передаточную функцию по возмущающему воздействию – статическому току двигателя.
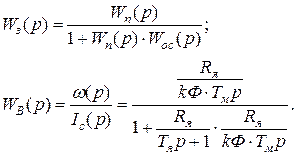
после преобразований получим:
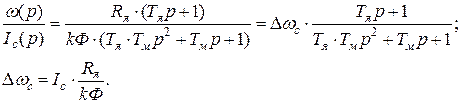
Аналогично случаю рассмотрения ПП по управляющему воздействия находятся корни характеристического уравнения (2.7).
Общее решение характеристического уравнения имеет вид:
- для случая действительных корней:
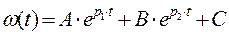
- для комплексных корней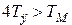 
:
, 
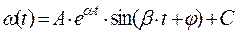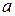- вещественная,
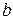- мнимая часть корня.
Коэффициенты определяются из начальных условий
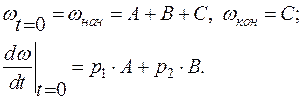
Но поскольку в числителе передаточной функции стоит составляющее с оператором р, то эти уравнения примут вид:
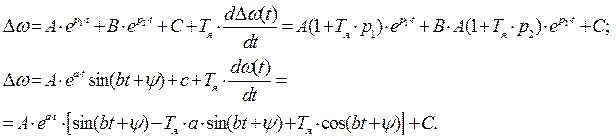
Начальными и конечными условиями являются:
при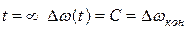 
;
при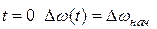
;
при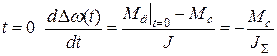 
.
Система для определения коэффициентов принимает вид:
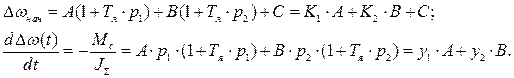
Решая систему, определяем коэффициенты.
Переходной процесс тока якоря можно получить продифференцировав выражение для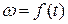 
:
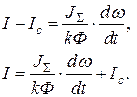
Расчет переходных процессов в замкнутой системе автоматического регулирования (САР)
Систему дифференциальных уравнений ДПТ можно привести к одному уравнению второго порядка
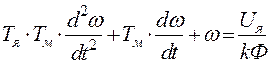, при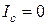 
.
Рассмотрим систему Т-ПД с ООС по скорости.
Ввиду малости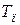 
, инерционностью ТП можно пренебречь.
Передаточная функция замкнутой САР:
.
Характеристическое уравнение замкнутой САР:
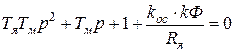, является естественным обобщением характеристического уравнения разомкнутой системы.
, 
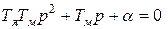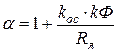
корни этого уравнения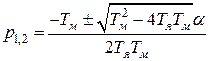 
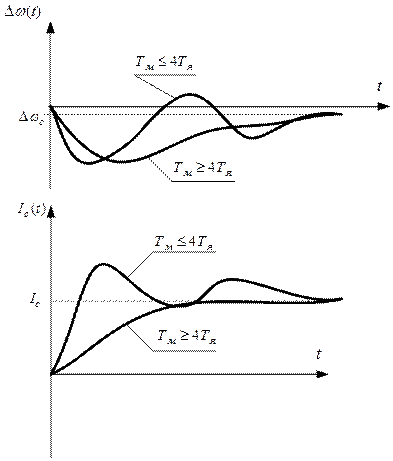
Вид ПП в разомкнутой и замкнутой САР.
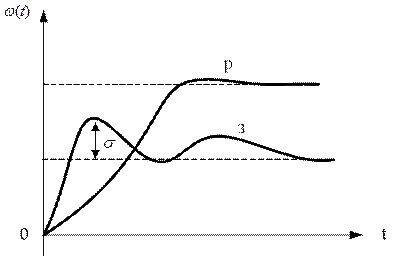
С ростом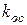 
увеличивается перерегулирование и уменьшается время регулирования.
