В класс НВ-моделей входят теория cтохастических дифференциальных уравнений и теория массового обслуживания [3].
Для задач исследования СУ наиболее подходящей концептуальной моделью служит теория массового обслуживания. которая применяется для построения математических моделей сложных систем управления отличающихся:
1) наличием потока многих заявок на выполнение определенных операций (заявок на обслуживание);
2) наличием многократно повторяемых операций (выходной поток).
Теория массового обслуживания разрабатывает и исследует математические модели различных по своей природе процессов функционирования экономических, производственных, технических и других систем, например: поставок сырья и комплектующих изделий некоторому предприятию; заданий, поступающих на ЭВМ от удаленных терминалов; вызовов в телефонных станциях и т.д. При этом для функционирования таких систем характерна стохастичность (случайность) моментов времени появления заявок на обслуживание.
Сложная система S, описываемая как система массового обслуживания (СМО), состоит из L 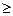 1 взаимосвязанных и взаимодействующих элементов-приборов обслуживания ПО1,… ПОl. Каждый прибор обслуживания ПОi состоит:
1 взаимосвязанных и взаимодействующих элементов-приборов обслуживания ПО1,… ПОl. Каждый прибор обслуживания ПОi состоит:
- из накопителя заявок Нi в котором могут одновременно находиться li заявок 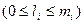 , mi - емкость накопителя Hi, т.е. число мест в очереди для ожидания начала обслуживания в канале.
, mi - емкость накопителя Hi, т.е. число мест в очереди для ожидания начала обслуживания в канале.
- канала Кi обслуживания заявок; Кi (i= 1, L).
На каждый элемент прибора ПОi поступают потоки событий; в накопитель Hi - поток заявок {vi}, на канал Ki - поток "обслуживаний" {ui}. Поток заявок {vi} представляет последовательность времени между моментами появления заявок на входе СМО и образует подмножество неуправляемых переменных СМО. Поток {ui} представляет собой последовательность интервалов времени между моментами начала и окончания обслуживания заявок и образует подмножество управляемых переменных. Заявки, обслуженные каналом Кi и заявки, покинувшие прибор ПОi по различным причинам необслуженными (например, из-за конечности mi или отсутствия времени на ожидание), образуют выходной поток {yi} - последовательность интервалов времени между моментами выхода заявок; это и есть выходной сигнал СМО.
Процесс функционирования прибора ПОi можно представить как процесс изменения состояний его элементов во времени
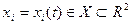 , где xi1(t) - число заявок, находящихся в накопителе в момент времени t, xi2(t) - состояние канала обслуживания Кi (xi2(t) = 0, если канал свободен, xi2(t) = 1, если канал занят).
, где xi1(t) - число заявок, находящихся в накопителе в момент времени t, xi2(t) - состояние канала обслуживания Кi (xi2(t) = 0, если канал свободен, xi2(t) = 1, если канал занят).
Приборы обслуживания ПО,..., ПОL, связаны и взаимодействуют между собой. Если каналы {Кi} различных приборов обслуживания соединены параллельно, то имеет место многоканальное обслуживание. Если же приборы {ПОi} или их параллельные блоки соединены последовательно, то имеет место многофазное обслуживание. Все сказанное представлено на рис.3.6.
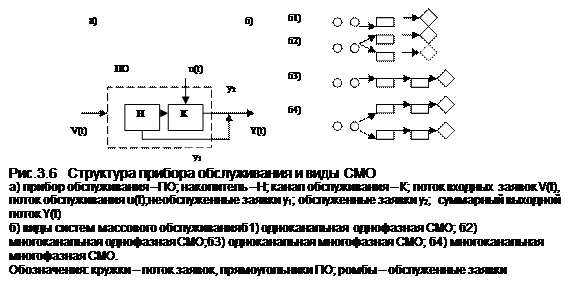
Для обозначения простых (однофазных) СМО используется символика, предложенная Кендаллом:
A/B/n/m.
Символ А характеризует входящий поток заявок:
-A = GI рекуррентный поток,
-A = М - простейший поток с показательным распределением вероятностей,
-А = Еk, - поток Эрланга k-го порядка;
-А = D - регулярный или детерминированный поток (с постоянными интервалами между моментами поступления заявок).
Символ В характеризует случайные последовательности длительностей обслуживания на отдельных каналах:
-В = G или B = GI - рекуррентное обслуживание с одной и той же функцией распределения B(t) для разных каналов;
- В = М - показательное обслуживание;
- В = Еk- эрланговское обслуживание k-го порядка;
- В = D- регулярное обслуживание.
Символ n означает количество обслуживающих каналов,
Символ m - количество мест для ожидания заявок в очереди.
Если n > 1, то система называется многоканальной. Значение m = 0 характеризует СМО с потерями; m = 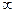 - систему с ожиданием; 0 < m <
- систему с ожиданием; 0 < m < 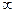 - систему с ограниченным числом мест для ожидания.
- систему с ограниченным числом мест для ожидания.
Рассмотрим пример, в котором имеется возможность аналитического определения показателей эффективности функционирования СМО (М/М/1).
Пусть процесс обслуживания начинается при отсутствии заявок в накопителе, тогда состояние СМО описывается следующей системой уравнений:
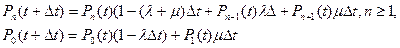
где Рn(t) - вероятность нахождения системы в состоянии 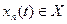 в момент t, т.е. когда в ней находятся n заявок.
в момент t, т.е. когда в ней находятся n заявок.
Вероятность нахождения в системе n заявок в момент времени (t + 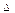 t) равна сумме трех вероятностей:
t) равна сумме трех вероятностей:
1) вероятности нахождения в системе n заявок в момент t, умноженной на вероятность того, что за время 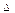 t в систему не поступает ни одной заявки и ни одна заявил не будет обслужена;
t в систему не поступает ни одной заявки и ни одна заявил не будет обслужена;
2) вероятности нахождения в системе (n - 1) заявки в момент t, умноженной на вероятность поступления одной заявки за время 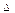 t, и ни одна заявка не будет обслужена;
t, и ни одна заявка не будет обслужена;
3) вероятности нахождения в системе (n + 1) заявки в момент t, умноженной на вероятность ухода одной заявки, при условии не поступления ни одной заявки.
Заметим что
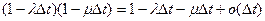
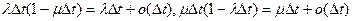
Образуя разностное уравнение и переходя к пределу, получаем дифференциальные уравнения:
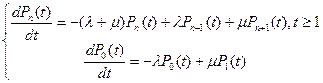
Найдем выражение среднего числа заявок, находящихся в накопителе, и среднего времени ожидания заявок в накопителе для стационарного состояния при загрузке 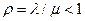
Приравняв производные по времени t к нулю, получим уравнения:
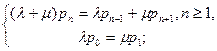
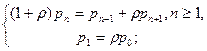
Положим n =1, тогда (1+ 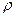 )p1 = p2 +
)p1 = p2 + 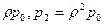 , повторяя эти операции, имеем рn =
, повторяя эти операции, имеем рn = 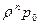 , причем
, причем
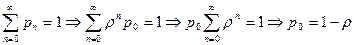 .
.
Следовательно, получим, что рn = рn(1 - 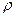 ) геометрическое распределение.
) геометрическое распределение.
Среднее число заявок в системе равно:
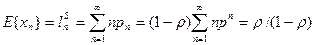 ,
,
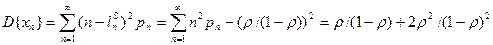 .
.
Среднее число заявок, находящихся в накопителе, равно
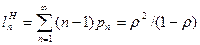 .
.
Среднее время ожидания заявок в накопителе равно
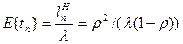 .
.
 2014-02-09
2014-02-09 1219
1219








