Б. Понятие модельного времени

Отметим две особенности функционирования ЭВМ, которые приходится учитывать при разработке ИМ сложных систем.

1. Сложная система S, как правило, состоит из многих элементов. Все элементы системы S функционируют одновременно. Однако в большинстве современных ЭВМ параллельное выполнение нескольких программ, имитирующих поведение отдельных элементов системы, невозможно.

2. Поскольку ИМ — это программы для ЭВМ, то они должны оперировать с конечным множеством данных и, следовательно, имитировать поведение системы S не во все моменты времени t 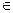[О, Т ], а лишь в некоторые, составляющие конечное множество 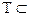[О, T], 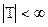(где 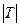означает мощность множества ),

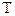Чтобы обеспечить имитацию параллельных (одновременных) событий системы S на конечном множестве моментов времени 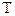, в ИМ используется специальная переменная t, называемая системным модельным временем или просто модельным временем (MB).

MB t следует отличать от других типов времени, используемых при ИМ систем, таких, как: t_p — реальное время системы S, функционирование которой имитируется; t_э — машинное время имитации, отражающее затраты ресурса времени ЭВМ на организацию имитационного моделирования.

Существуют два способа формирования конечного множества моментов времени 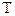, известных как принципы организации изменения модельного времен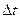и "" и "".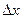

"Принцип 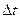" заключается в изменении MB с фиксированным шагом .

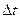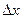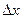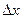
"Принцип " заключается в изменении MB при скачкообразном изменении вектора состояния х системы S на некоторую величину (0).

Для моментов времени t* из множества 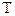, сформированного по принципу "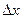", справедливо

x(t* + 0) = х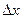(t*) + , t* .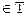

Для моментов времени из множества [О, T] \ 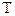вектор состояний изменяется непрерывно (либо остается неизменным).

Заметим, что скачкообразные изменения состояния системы S происходят при наступлении таких "особых" событий, как поступление управляющих сигналов и внешних воздействий, выдача выходных сигналов и т.п.

Приведем более строгое описание принципов "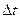" и "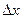" и поясним их особенности. Пусть СС S состоит из N элементов: A⁽¹⁾,..., А ^(N) поведение которых предполагается моделировать:

S={A⁽¹⁾,...,А^(N))}.

Для каждого элемента А⁽ⁱ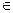⁾ S (i = 1 ,..., N) определим локальное модельное время (ЛМВ) t⁽ⁱ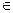⁾ [О, T]. Поведение элемента А⁽ⁱ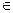⁾ S в течение интервала моделирования определяется некоторой последовательностью действий

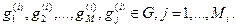
где G — множество всевозможных действий для элементов S. На множестве G будем выделять подмножество действий D: D 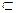G, для выполнения которых в ИМ требуется некоторое ненулевое модельное время.

Будем обозначать такие действия 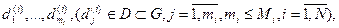, а интервалы модельного времени, затрачиваемые на выполнение этих действий, соответственно: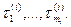. Последовательность {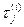} (j=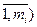) является последовательностью случайных величин с заданными законами распределения L{ 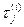}, i=.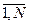

Действия {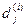} D приводят к наступлению в системе S особых событий {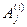}. События {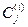}, к которым приводят действия {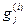}: {} 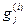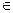G \ D, не требующие затрат MB, считаются неособыми.

Момент ЛМВ наступления событи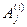я для 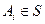определяется по формуле:

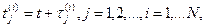(3.5)

где 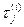имитируется на ЭВМ в соответствии с законом распределения L{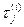}, t*— текущее значение MB.

Состояние системы S в момент времени t 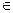[0, Т] определяется вектором состояния x(t) 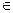X 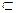Rⁿ. Состояния системы в моменты наступления особых событий будем называть особыми состояниями, а состояние x (0) — начальным состоянием системы.

Для иллюстрации принципов "" и "" используем временную диаграмму, изображенную на рис.3.7

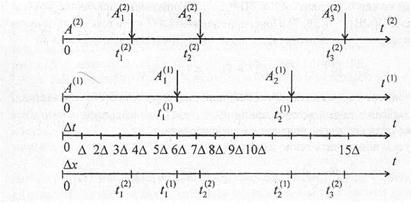Рис. 3.7 Временная диаграмма

Описание временной диаграммы.

Пусть число моделируемых элементов в S равно 2, т.е. N = 2, и S = {A⁽¹⁾, A⁽²⁾}.

Временная диаграмма включает:

— временную ось ЛМВ t ⁽¹⁾для элемента А ⁽¹⁾,

— временную ось ЛМВ t ⁽²⁾ для элемента А ⁽²⁾,

— временную ось модельного времени по принципу "";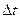

— временную ось модельного времени по принципу "".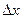

Временные оси будем помечать символами ”А⁽¹⁾”, ”А⁽²⁾”, ""; "".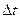

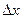Пусть в течение рассматриваемого интервала моделирования

[0, Т] для элемента А ⁽¹⁾ произошло 2 события: 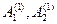в моменты 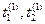, для элемента A ⁽²⁾ — 3 события: 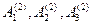в моменты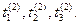

Предположим, что хронологическая последовательность событий такова:

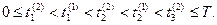
Принцип " ".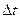

В соответствии с принципом " 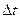" изменение модельного времени t происходит через промежутки времени, равные 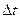, т.е. t в течение времени моделирования Т принимает конечное множество значений:

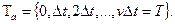
При этом событиям, которые попадают в интервал постоянства MB 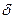_r = ((r - 1 )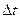, rt), r = 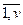, в ИМ присваивается один и тот же момент наступления: t = rt. Выбор величины t существенно влияет как на быстродействие ИМ, так и на точность аппроксимации СС S с помощью ИМ. Пусть t выбран таким, как указано на диаграмме (рис.2.1), т.е. моменты наступления событий в S принадлежат следующим интервалам:

,

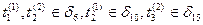Это означает, что соответствующим событиям в ИМ будут присвоены следующие моменты наступления:

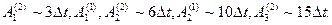
При этом фазовая траектория системы S с вектором состояний x(t) 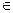X будет иметь вид:

х(0), x(t) = x(2t) = x(0), x(3t) = х(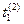), x(4t) = x(5t) = x(3t),

x(6t) = х(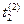), x(7t) = x(8t) = x(9t) = x(6t), x(10t) = x(),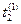

x(11t) =...=x(14t) = x(10t), x(15t) = x().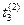

На основании полученной фазовой траектории можно сделать следующие выводы относительно выбора t:

1) если t — мало, то выполняется много лишних вычислений состояний системы в моменты, когда вектор x(t) не изменяется (за счет этого возрастает t_э выполнения ИМ);

2) даже при сравнительно малом значении t моменты наступления событий в системе (а следовательно, и моменты изменения состояния системы) не совпадают с моментами наступления событий в ИМ, поэтому фазовая траектория, построенная с помощью ИМ, на множестве 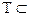[0, Т] не совпадает с фазовой траекторией системы S.

Принцип ”х".

В соответствии с принципом "х" изменение модельного времени происходит в моменты наступления событий или, что то же самое, в моменты особых состояний, т.е. для нашего примера:

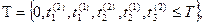
а фазовая траектория, построенная с помощью ИМ, будет совпадать на множестве 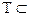[0, Т] с фазовой траекторией системы S:

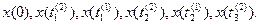
Приведем более строгие формулировки правил изменения MB по принципам "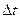" и "".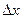

Пусть t* < Т — некоторый момент особого состояния системы S;

r_i — число событий, произошедших с элементом 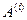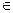S до момента t* включительно (i = 1,..., N)',

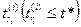— момент наступления последнего для элемента А⁽ⁱ⁾ события до момента t* включительно;

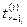> t* — момент наступления ближайшего после r_i будущего события;

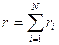— общее число событий в момент t*

t** и 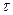**— моменты ближайших будущих событий в ИМ, вычисленные по принципам "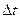" и "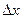" соответственно.

Модельное время t в ИМ можно рассматривать как функцию от числа событий, происходящих в ИМ. Очевидно: t(r) = = t* < Т, r = 0, 1, 2,...,

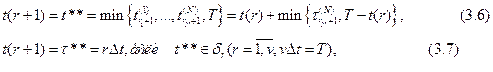
где {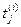}, {} 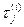определяются соотношением (3.5) Заметим, что

моменты МB t** = Т 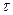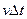и ** = (если 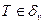) являются моментами завершения моделирования.

Правила (3.6) и (3.7) называются правилами изменения модельного времени по принципам "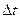" и "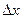" соответственно.

Пример. Проиллюстрируем эти правила с. помощью рис. 3.7

Пусть 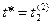, тогда r₁=1, r₂=2, r=r₁+r₂ = 3, t(4)=t**=min 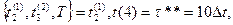так как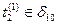

На практике отдается предпочтение принципу "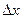". Принцип "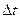" используется лишь в случаях, когда:

1) события {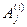} таковы, что 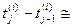const на всем интервале моделирования Т, и, следовательно, можно подобрать интервал 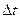изменения MB, обеспечивающий минимальную погрешность аппроксимации (например, для разностных уравнений);

2) событий очень много и они появляются группами. В этом случае за счет групповой обработки событий 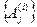, попавших внутрь очередного шага изменения 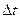, удается уменьшить затраты машинного времени.

В большинстве практически важных случаев события 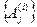наступают через случайные интервалы времени 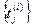. Поэтому способ задания шага до следующего события экономичнее (в смысле затрат машинного времени) и точнее (в смысле точности аппроксимации) фазовой траектории способа фиксированного изменения МВ.