2014-02-09
741
Пусть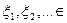 
[О, 1) — независимые одинаково распределенные случайные величины; N — натуральное число; определены случайные величины:
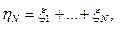
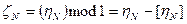(3.28)
Сформулируем результат, выражающий свойство воспроизводимости равномерного закона.
Теорема 3.2. Если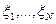 
имеют равномерное распределение, то и случайная величина 
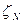имеет стандартное равномерное распределение R [0, 1).
Доказательство. По правилам функционального преобразования (3.28) случайных величин выразим плотность распределения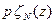 
случайной величины 
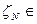[О, 1) через плотность 
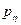(у) распределения величины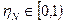 
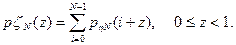(3.29)
Методом математической индукции (с использованием формулы свертки распределений) находим
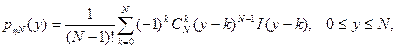(3.30)
где I(u) — единичная функция Хэвисайда.
Подставляя теперь (3.30) в (3.29), заменяя индекс суммирования i на j= i - k и меняя порядок суммирования по j, k, получаем
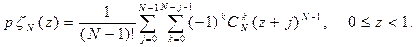
Суммируя по k и учитывая тождество
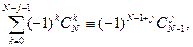
находим
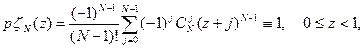
что и требовалось доказать.
Доказанное свойство позволяет строить весьма эффективные датчики на ПЭВМ. Пусть имеется два простейших датчика БСВ Д1, Д2; {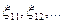
}, {
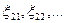} — независимые случайные последовательности, имитируемые этими датчиками; р
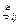(х) — плотность распределения случайной величины 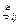, х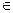 
[0, 1) (i = 1, 2; j = 1, 2,...). Пусть 
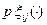отличается
от плотности стандартного распределения
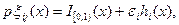(3.30)
где h(·) — ограниченная функция, такая, что
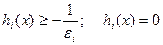при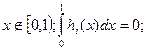 
(3.31)
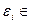[ 0, 1) и характеризует точность датчика Д1: чем 
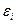меньше, тем точность выше.
Теорема 3.3. Пусть аналогично (3.28)
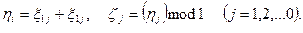(3.32)
Если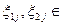 
[О, 1) независимы и имеют плотности (4.48), то 
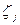, имеет плотность распределения
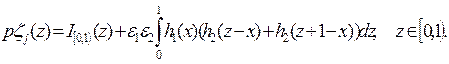(3.33)
Доказательство. Согласно 3.32
),
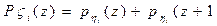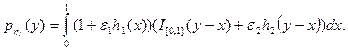
Поэтому при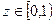 
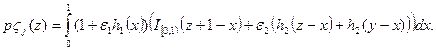
Подинтергальное выражение упрощается, поскольку
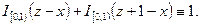
Тогда с учетом (4.49) получаем (4.51).
Из сравнения (4.48) заключаем, что случайная последовательность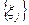 
имеет распределение, более близкое к R[0,1), чем 
:
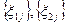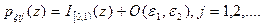
Формула (3.33) используется для получения j-го псевдослучайного числа. Аналогичным образом, увеличивая число исходных датчиков Д1, Д2, …, можно достичь требуемой точности моделирования.
В заключение отметим еще, что для увеличения отрезка апериодичности последовательности следует использовать датчики Д1, Д2, периоды у которых Т1, Т2 – взаимно простые числа.
