2014-02-09
1420
Рассмотрим теперь основные методы и алгоритмы, используемые при построении программных датчиков БСВ.
1. Мультипликативный конгруэнтный метод (метод вычетов)
Согласно этому методу псевдослучайная последовательность вычисляется по рекуррентным формулам
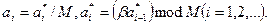(3.25)
где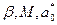 
параметры программного датчика (натуральные числа): 
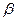— множитель, М — модуль, 
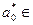{1,..., М - 1} — стартовое значение, операция у = (z) modM означает вычет числа z по модулю М:
у = z - М [ z/М ].
Из (3.25) следует: 1) последовательность {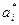
}, а значит и
{аi}, всегда зацикливается, т.е. начиная с некоторого номера i0 образуется цикл, который повторяется бесконечное число раз;
2) период последовательности Т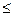 
М - 1 (если 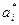= 0, то 
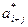= 0 для любого 
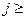1).
Параметры μ, М, 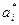выбираются из условия максимума периода. Период Т можно определить аналитически методами теории чисел или с помощью численных экспериментов на ЭВМ. Например, часто используется типовой программный датчик RANDU. В табл. 3.5 приведены данные для двух вариантов датчика соответствующих 32-разрядной ЭВМ (машинное слово содержит q = 32 разряда) и 16-разрядной ЭВМ (q = 16).
|
|
|
Таблица 3.5
| q | M | β |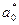 
| T |
| 231 = 2147483648 | 216 + 3 = 65539 | М/4 = 36870912 | ||
| 215 = 32768 | 28 + 3 = 259 | М/4 = 8192 |
2. Метод, использующий линейные смешанные формулы.
В этой ситуации псевдослучайная последовательность вычисляется рекуррентно по так называемой линейной смешанной формуле, обобщающей (3.25):
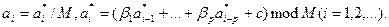(3.26)
Параметры датчика: р — порядок;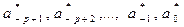 
—
стартовые значения;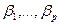 
— множители; с — приращение; М — модуль. Период датчика Т 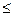МР - 1, т.е. растет с увеличением М и p.
