2014-02-24
850
Определение 3: гомотетия с центром S и коэффициентом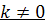 
называется преобразование пространства 
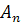, при котором образом любо точки M является такая точка M’, что 
.
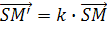Пусть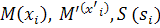 
, тогда по определении гомотетии 
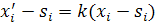или
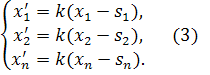
Если S =0, то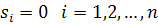 
и формулы (3) принимают вид 
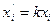(4).
Формулы гомотетии являются частным случаем формул (1) из §8 при
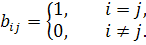
Следовательно, гомотетия является аффинным преобразованием, а ассоциированное с ним векторное преобразование формулами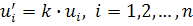 
.
Обозначим гомотетию с центром S и коэффициентом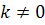
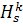, тогда, очевидно: 
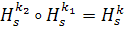, где 
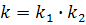и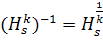 
. Следовательно, гомотетии с общим центром пространства 
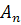образуют группу, являющуюся группой аффинных преобразований этого пространства.
