2014-02-24
1073
Определение 1: пусть пара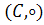
– группа и 
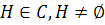. Если пара 
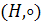сама является группой, то она называется подгруппой группы 
.
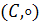Определение 2: преобразование пространства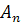 
называется параллельным переносом на данный вектор 
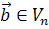, если образом любой точки М является такая точка
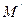, что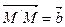 
.
Пусть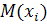 
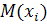, b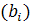 
, тогда по определению параллельного переноса имеем:
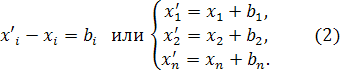
Формулы (2) являются частным случаем формул (1) из §8 при
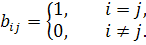
По теореме (2) из §8 параллельный перенос является аффинным преобразованием. По следствию из этой теоремы ассоциированное с ним векторное преобразование выражается формулами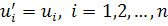 
, следовательно, является тождественным преобразованием.
Обозначим параллельный перенос на вектор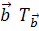 
, тогда, очевидно: 
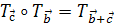и 
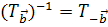. Следовательно, параллельные переносы пространства 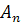образуют группу, являющуюся подгруппой группы аффинных преобразований этого пространства.
