Уравнение (4) из §20 при m=n-1 принимает вид:
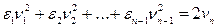 (3)
(3)
где все 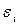 равны
равны 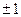 .
.
Квадрика называется параболоидом, она не имеет ни одного центра (является нецентральной), что вытекает из замечания (2) §20.
Примеры:
7) n=2, уравнение 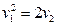 задаёт на аффинной плоскости
задаёт на аффинной плоскости 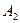 параболу с вершиной
параболу с вершиной 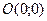 и осью
и осью 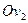 ,
, 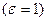 .
.
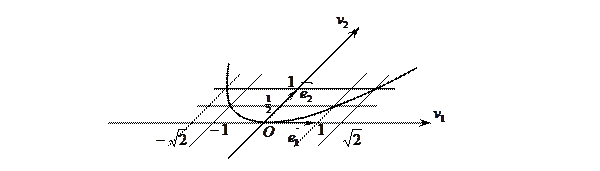
Аналогично при 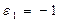 имеем параболу
имеем параболу 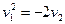
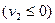 .
.
8) n=3, поверхности пространства 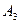 :
:
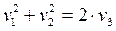 - эллиптический параболоид
- эллиптический параболоид
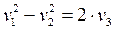 - гиперболический параболоид
- гиперболический параболоид
(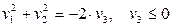 ;
; 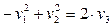 )
)
IV. Цилиндрические квадрики (цилиндры)
Рассмотрим теперь случаи, когда в уравнениях (2) и (3) из §20 m<n, а в уравнении (4) из §20 m<n-1. Положим в уравнении (2) и (3) m=r, а в уравнении (4) m=r-1. Получим следующие уравнения:
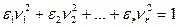 (4)
(4)
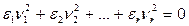 (5)
(5)
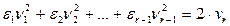 (6)
(6)
где r<n и все 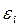 равны
равны 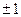 .
.
Квадрики с такими уравнениями называются цилиндрическими (цилиндрами).
Замечание 4:Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (n-r) – мерных плоскостей, называемых образующими, пересекающих некоторую квадрику, называемую направляющей и лежащей в r – мерной плоскости 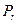 . Квадрики с уравнениями (4) и (5) имеют бесконечноемножество центров, являющееся (n-r)-мерной плоскостью. Так как переменная
. Квадрики с уравнениями (4) и (5) имеют бесконечноемножество центров, являющееся (n-r)-мерной плоскостью. Так как переменная 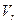 содержится в уравнении в первой степени, изменение её знака приводит к другому уравнению, следовательно, (6) центров не имеет.
содержится в уравнении в первой степени, изменение её знака приводит к другому уравнению, следовательно, (6) центров не имеет.
|
|
|
Примеры:
9) n=2, линии аффинной плоскости 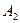 :
:
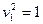 - пара различных параллельных оси
- пара различных параллельных оси 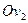 прямых. Образующими являются две прямые с уравнениями
прямых. Образующими являются две прямые с уравнениями 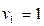 и
и 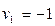 , а направляющие – пара точек A(1;0) и B(-1;0), в которых эти прямые пересекают ось
, а направляющие – пара точек A(1;0) и B(-1;0), в которых эти прямые пересекают ось 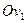 с уравнением
с уравнением 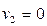 .
.
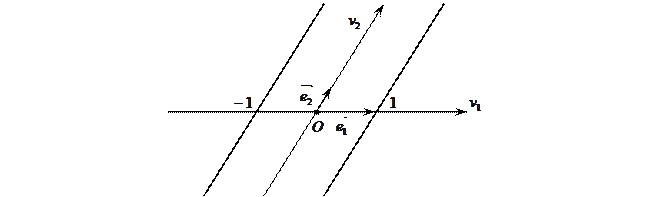
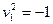 - пара мнимых прямых, параллельных оси
- пара мнимых прямых, параллельных оси 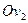 .
.
10) n=3, поверхности пространства 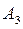 .
.
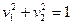 - эллиптический цилиндр.
- эллиптический цилиндр.
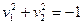 - мнимый эллиптический цилиндр.
- мнимый эллиптический цилиндр.
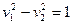 - гиперболический цилиндр.
- гиперболический цилиндр.
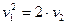 - параболический цилиндр.
- параболический цилиндр.
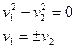 - пара пересекающихся плоскостей.
- пара пересекающихся плоскостей.
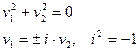 - пара мнимых плоскостей, пересекающихся по действительной прямой с уравнениями
- пара мнимых плоскостей, пересекающихся по действительной прямой с уравнениями 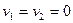 .
.
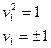 - пара различных параллельных плоскостей.
- пара различных параллельных плоскостей.
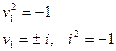 - пара мнимых параллельных плоскостей.
- пара мнимых параллельных плоскостей.
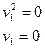 - пара совпадающих плоскостей.
- пара совпадающих плоскостей.
Остальные случаи сводятся к рассмотренным изменением нумерации координат.
Замечание 5: Сопоставление рассмотренных выше примеров показывает, что все квадрики пространства 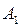 разбивается на три класса, пространства
разбивается на три класса, пространства 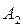 - на девять классов, пространства
- на девять классов, пространства 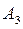 - на семнадцать классов. В один класс при этом объединяются все квадрики, уравнения которых с помощью надлежащего выбора аффинной системы координат можно привести к одинаковому виду. Любые две квадрики одного класса аффинно-эквивалентны, так как формулы перехода от одной системы координат к другой и формулы аффинного преобразования пространства
- на семнадцать классов. В один класс при этом объединяются все квадрики, уравнения которых с помощью надлежащего выбора аффинной системы координат можно привести к одинаковому виду. Любые две квадрики одного класса аффинно-эквивалентны, так как формулы перехода от одной системы координат к другой и формулы аффинного преобразования пространства 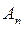 с алгебраической точки зрения имеют один и тот же вид.
с алгебраической точки зрения имеют один и тот же вид.
Замечание 6: Квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому аффинно-эквивалентными могут оказаться и квадрики из различных классов. С геометрической точки зрения эти классы не различаются между собой.
|
|
|
 2014-02-24
2014-02-24 818
818








