Пусть в аффинном пространстве An квадрика заданна в некоторой аффинной системе координат уравнением:
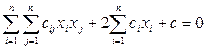 ,
, 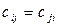 . (1)
. (1)
Даже при небольших значениях n уравнение (1) является громоздким. Упростить это уравнение путём надлежащего выбора системы координат позволяет следующая основная теорема.
Теорема 1:При соответственном выборе аффинной системы координат уравнение (1) любой квадрики в An может быть приведено к одному и только одному из следующих видов:
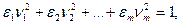 где
где 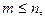 (2)
(2)
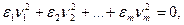 где
где 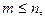 (3)
(3)
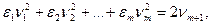 (4)
(4)
где 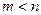 , а числа
, а числа 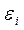 всюду равны +1 или -1.
всюду равны +1 или -1.
□ [5] Т. с. 83-85.
Определение 5: Уравнения (2), (3) и (4) называются нормальными видами уравнения квадрики.
Теорема 2:Если уравнение квадрики имеет вид (2) или (3), то точка S(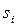 ), для которой
), для которой 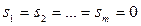 , является центром квадрики.
, является центром квадрики.
□ Если точки 
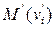 и
и 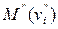 , симметричны относительно точки S, то
, симметричны относительно точки S, то 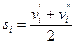 или
или 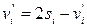 . По условию
. По условию 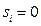 , для
, для 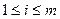 , тогда
, тогда 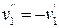 ,
,
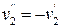 ,...,
,..., 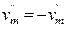 . Очевидно, если координаты точки
. Очевидно, если координаты точки 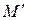 удовлетворяют уравнениям (2) или (3), то ему же и удовлетворяют координаты точки
удовлетворяют уравнениям (2) или (3), то ему же и удовлетворяют координаты точки 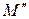 ,то если точка
,то если точка 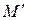 принадлежит квадрике, то и точка
принадлежит квадрике, то и точка 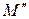 ей принадлежит. По определению (3) §19 точка S – центр данной квадрики. ■
ей принадлежит. По определению (3) §19 точка S – центр данной квадрики. ■
Замечание 1:Из теоремы (2) следует, что все точки (n-m) – мерной плоскости 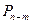 , задаваемой уравнением
, задаваемой уравнением 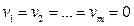 , являются центрами квадрики (2) или (3). Других центров эти квадрики не имеют. При m=n плоскость является нуль - мерной и совпадает с началом координат
, являются центрами квадрики (2) или (3). Других центров эти квадрики не имеют. При m=n плоскость является нуль - мерной и совпадает с началом координат 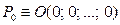 .
.
Замечание 2: В уравнении (4) переменная 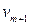 содержится в первой степени, при замене
содержится в первой степени, при замене 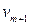 на
на 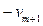 уравнение (4) изменится, значит, квадрика с таким уравнением не имеет ни одного центра.
уравнение (4) изменится, значит, квадрика с таким уравнением не имеет ни одного центра.
Замечание 3: Согласно теореме (1) для любой квадрики имеет место один и только один случай:
1) квадрика не имеет центра (неустойчивая);
2) квадрика имеет единственный центр (центральная);
3) квадрика имеет бесконечное множество центров (с многомерной плоскостью центров).
§21.Классификация квадрик в пространстве A n
I. Эллипсоиды и гиперболоиды
Уравнение (2) из §20 при m=n принимает вид:
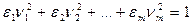 , (1)
, (1)
Числа 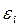 равны
равны 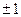 .
.
В зависимости от знаков 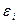 получаются квадрики разных видов.
получаются квадрики разных видов.
1) При 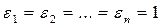 квадрика называется эллиптической и имеет уравнение
квадрика называется эллиптической и имеет уравнение 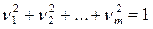 .
.
Замечание 1: В аффинной геометрии отсутствует понятие расстояния между точками, поэтому нет и понятия сферы и эллипсоида вращения.
2) При 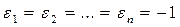 уравнение (1) имеет вид:
уравнение (1) имеет вид: 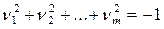 и определяет пустое множество точек, но по аналогии с предыдущем случаем называется мнимым эллипсоидом.
и определяет пустое множество точек, но по аналогии с предыдущем случаем называется мнимым эллипсоидом.
3) Если числа 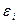 не все одинаковы, то квадрика называется гиперболоидом.
не все одинаковы, то квадрика называется гиперболоидом.
Замечание 2: Согласно теореме (2) из §20 эллипсоиды и гиперболоиды с уравнением (1) являются центральными квадриками; их центр совпадает с началом координат.
Примеры:
1) n=1
Для аффинной прямой A1 имеем уравнение 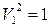 и
и 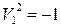 , задающие соответственно пару точек и пустое множество.
, задающие соответственно пару точек и пустое множество.
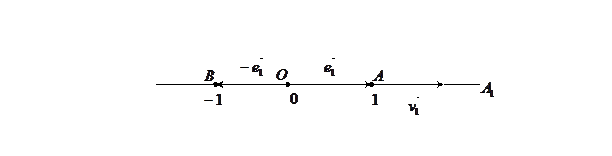
2) n=2, квадрики аффинной плоскости:
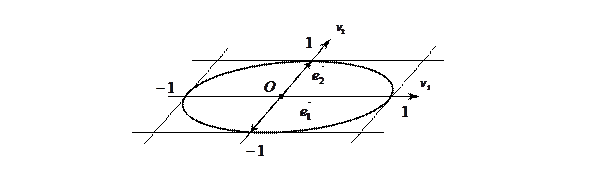
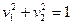 - эллипс
- эллипс
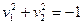 - мнимый эллипс
- мнимый эллипс
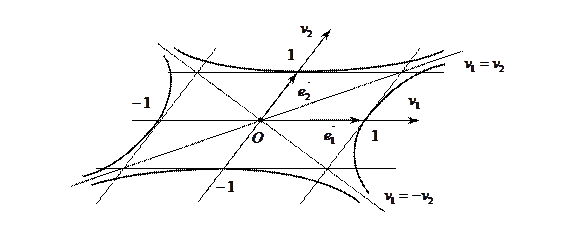
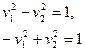 - гиперболы, взаимно сопряжённые.
- гиперболы, взаимно сопряжённые.
3) n=3, квадрики пространства 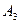 :
:
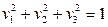 - эллипсоид
- эллипсоид
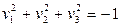 - мнимый эллипсоид
- мнимый эллипсоид
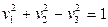 - однополостный гиперболоид
- однополостный гиперболоид
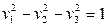 - двуполостный гиперболоид
- двуполостный гиперболоид
В остальных случаях следует изменить нумерацию координат.
II. Конические квадрики (конусы)
Уравнение (3) из §20 при m=n принимает вид:
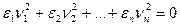 (2)
(2)
где все 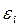 равны
равны 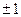 .
.
1) Если значения 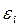 не все одинаковы, то квадрика называется конусом. Это центральная квадрика, её центр совпадает с началом координат и называется вершиной.
не все одинаковы, то квадрика называется конусом. Это центральная квадрика, её центр совпадает с началом координат и называется вершиной.
Замечание 3: Если координаты точки 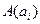 , отличной от вершины конуса, удовлетворяют уравнению (2), то ему удовлетворяют так же координаты любой точки вида
, отличной от вершины конуса, удовлетворяют уравнению (2), то ему удовлетворяют так же координаты любой точки вида 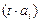 ,
, 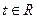 . Множество всех таких точек является прямой, проходящей через точку A и вершину конуса – начало координат. Эта прямая называется его прямолинейной образующей.
. Множество всех таких точек является прямой, проходящей через точку A и вершину конуса – начало координат. Эта прямая называется его прямолинейной образующей.
2) Если 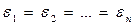 , то имеем уравнение
, то имеем уравнение 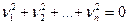 . Квадрика состоит, лишь из одной точки (начало координат) и называется мнимым конусом с вершиной в этой точке.
. Квадрика состоит, лишь из одной точки (начало координат) и называется мнимым конусом с вершиной в этой точке.
Примеры:
4) n=1: 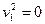 - пара точек аффинной прямой
- пара точек аффинной прямой 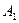 , совпадающих с началом координат.
, совпадающих с началом координат.
5) n=2, квадрики аффинной плоскости 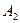 .
.
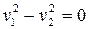 или
или 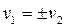 - пара пересекающихся в начале координат прямых.
- пара пересекающихся в начале координат прямых.
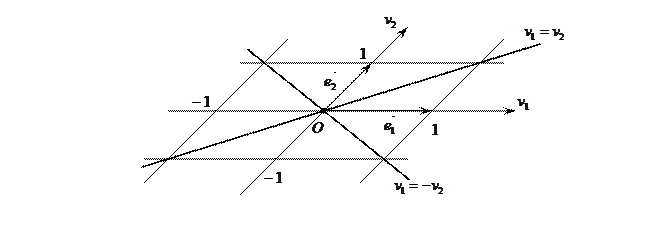
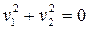 или
или 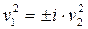 ,
, 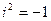 - пара мнимых прямых, пересекающихся в действительной точке
- пара мнимых прямых, пересекающихся в действительной точке 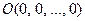 .
.
6) n=3, квадрики пространства 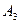
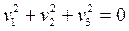 - мнимый конус (точка О),
- мнимый конус (точка О),
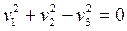 - конус (с вершиной в точке О).
- конус (с вершиной в точке О).
 2014-02-24
2014-02-24 2436
2436








