Определение 1: Линейное отображение векторного пространства 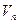 в себя называется линейным оператором:
в себя называется линейным оператором:
1) 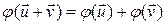 , 2)
, 2) 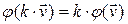 ,
, 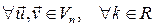 .
.
Определение 2: Линейный оператор  евклидового векторного пространства
евклидового векторного пространства 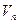 называется симметрическим, если
называется симметрическим, если
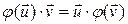 для
для 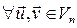 . (1)
. (1)
То есть, символ симметрического оператора при скалярном умножении можно перенести одного вектора на другой.
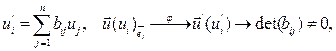 если
если  - биекция
- биекция
Теорема 1: симметрический линейный оператор в любом ортонормированном базисе имеет симметрическую матрицу.
□ Пусть симметрический линейный оператор  имеет в ортонормированном базисе
имеет в ортонормированном базисе 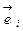 матрицу
матрицу 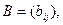
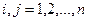 . Положим в формуле (1)
. Положим в формуле (1) 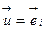 и
и 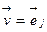 , тогда
, тогда 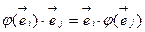 (2)
(2)
Так как векторы 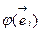 также являются базисными и выражаются через вектора
также являются базисными и выражаются через вектора 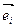 с помощью матрицы
с помощью матрицы 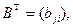 то имеем:
то имеем:
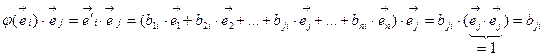 (3) - вследствие ортогональности базиса.
(3) - вследствие ортогональности базиса.
Аналогично получаем
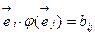 (4)
(4)
Из равенств (2), (3), (4) следует, что 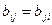 для любых
для любых 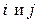 , то есть матрица
, то есть матрица 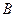 - симметрическая. ■
- симметрическая. ■
Теорема 2(обратная): если линейный оператор хотя бы в одном ортонормированном базисе имеет симметрическую матрицу, то он является симметрическим.
хотя бы в одном ортонормированном базисе имеет симметрическую матрицу, то он является симметрическим.
□ Пусть в ортонормированном базисе 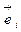 матрица
матрица 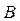 линейного оператора
линейного оператора  симметричная:
симметричная: 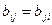 (5)
(5)
Тогда для 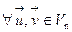 получаем:
получаем:
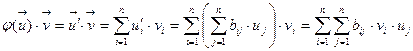 (6)
(6)
и 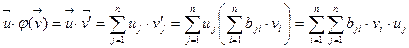 (7)
(7)
Из равенств (5), (6), (7) следует, что 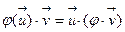 , то есть оператор
, то есть оператор  - симметрический. ■
- симметрический. ■
Теорема 3: характеристическое уравнение 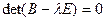 симметрического линейного оператора
симметрического линейного оператора  может иметь только действительные корни
может иметь только действительные корни 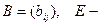 матрицы,
матрицы, 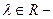 собственное значение вектора
собственное значение вектора 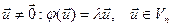 □■
□■
Следствие: любой симметрический линейный оператор имеет хотя бы одно собственное значение.
Замечание 2: согласно основной теореме алгебры любое алгебраическое уравнение имеет хотя бы один комплексный корень. В частности, характеристическое уравнение симметрического линейного оператора обладает этим свойством. По теореме 3 это число 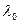 - действительное, оно является собственным значением данного оператора. Числа
- действительное, оно является собственным значением данного оператора. Числа  , являются решениями векторного уравнения
, являются решениями векторного уравнения 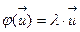 , также действительны и представляют собой координаты собственного вектора
, также действительны и представляют собой координаты собственного вектора 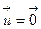 , соответствующего собственному значению
, соответствующего собственному значению 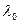 .
.
Теорема 4: собственные векторы симметрического линейного оператора, соответствующие его различным собственным значениям, ортогональны между собой.
□ Пусть 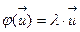 и
и 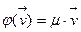 причем
причем 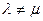 . Так как
. Так как  - симметрический линейный оператор, то
- симметрический линейный оператор, то 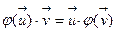
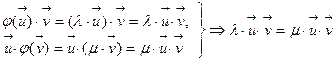 или
или 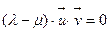 .
.
Так как 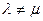 , то
, то 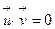 или
или 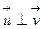 . ■
. ■
Теорема 5: для любого симметрического линейного оператора евклидова векторного пространства 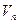 существует ортонормированный базис, составленный из собственных векторов этого оператора.
существует ортонормированный базис, составленный из собственных векторов этого оператора.
□ [5], с. 99-100, Т.2 (метод математической индукции).
Следствие: матрица симметрического линейного оператора с помощью соответствующего выбора ортонормированного базиса может быть приведена к диагональному виду; этот базис состоит из нормированных собственных векторов данного оператора.
 2014-02-24
2014-02-24 4885
4885








