Квадрики в евклидовом пространстве

1º. Упрощение уравнения квадрики

Определение квадрики, данное в §20 для аффинного пространства 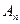, сохраняется и для евклидова пространства 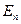. Но теперь уже используется только прямоугольные декартовы системы координат.

Пусть квадрика задана относительно ортонормированной системы координат 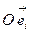общим уравнением вида: 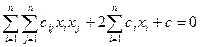(1), где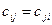

Вначале производится линейное ортогональное преобразование переменных приводящее к каноническому виду квадратичную форму из левой части уравнения (1) (см.§23). Пусть оно имеет вид: 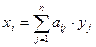(2), где .

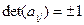С геометрической точки зрения это означает переход к новой прямоугольной декартовой системе координат, получаемой из исходной с помощью вращения вокруг начала координат. Уравнение (1) квадрики примет вид:

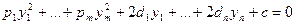(3)

где 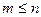и коэффициенты 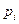не равны нулю.

Выделим полные квадраты:

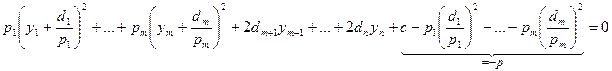(4)

Подвергнем систему координат параллельному переносу

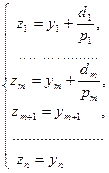(5) - это ортогональное преобразование ().

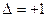Вводя обозначение 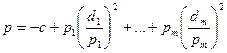, получаем уравнение квадрики в новой ортонормированной системе координат:

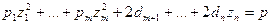, (6)

где 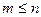и коэффициенты 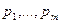отличны от нуля.

При дальнейшем упрощении этого уравнения в общем случае уже не удается добиться того, чтобы все коэффициенты при квадратах координат были равны 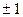, так как при помощи отрицательного преобразования квадратичная форма не всегда приводится к нормальному виду. Поэтому в пространстве E_n уравнение квадрики в общем случае уже не удается привести к такому простому виду, как в пространстве A_n (нормальному виду).

Замечание 1: так как равные фигуры является также аффинно-эквивалентными, то проведённая в §21 аффинная классификация квадрик имеет место и в пространстве E_n. Однако не всякие аффинно-эквивалентные фигуры равны, поэтому каждый класс аффинной классификации разбивается на бесконечное множество классов так, что любые две квадрики из одного класса равны, а любые две квадрики из разных классов не равны. То есть в пространстве E_n появляются новые виды квадрик, отсутствующие в пространстве А_n.

2º. Классификация квадрик в трёхмерном евклидовом пространстве

Дадим полную классификацию квадрик в пространстве Е₃ , для этого рассмотрим все частные случаи упрощения уравнения (6). .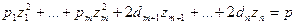

Случай 1: m=n=3, p ≠ 0.

Уравнение (6) принимает вид:

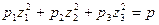или

.

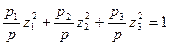В зависимости от знаков чисел p₁, p₂, p₃ и p уравнение принимает различные виды.

а) 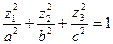– эллипсоид.

Так как не всякие два эллипсоидаравны и даже подобны, в евклидовой геометрии (см. опр. (3) §14) имеется возможность классификации эллипсоидов и других квадрик (при n=3 поверхностей 2-го порядка). Если a≠ b≠ c, то эллипсоид называется трёхосным. Если равны какие - либо две из чисел a, b, c, то имеем эллипсоид вращения. Если же a=b=c, то эллипсоид является сферой. Эта классификация инвариантна относительно движений пространства E_n.

б) 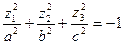– мнимый эллипсоид.

в) 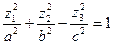– однополостный гиперболоид (при a=b - о.г. вращения).

г) 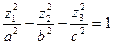- двуполостный гиперболоид (при a=с – д.г. вращения).

Случай 2:m=n=3, p=0.

Уравнение (6) принимает вид:

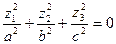
Возможны частные случаи:

а) 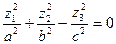– конус (при a=b – конус вращения).

б) 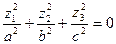– мнимый конус с вершиной в начале координат.

Случай 3: n=3, m=2, d₃≠0.

Уравнение (6) принимает вид:

. .

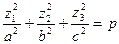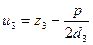Освободимся от свободного члена p с помощью параллельного переноса системы координат по формулам:

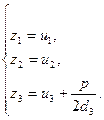
Получим уравнение: 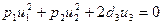и его частные случаи:

а) 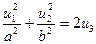– эллиптический параболоид (при a=b – э.п. вращения).

б) 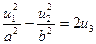– гиперболический параболоид (или седловая поверхность).

Случай 4 (цилиндры 2-го порядка):

I. .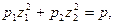

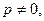
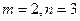а) 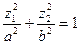- эллиптический цилиндр (при 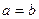- цилиндр вращения или

прямой круговой цилиндр).

б) 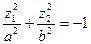- мнимый эллиптический цилиндр .

в) 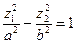- гиперболический цилиндр.

II.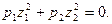

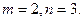
а) 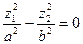- пара пересекающихся по оси 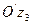плоскостей.

б) 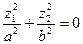- пара мнимых плоскостей, пересекающихся по оси .

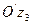III.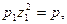

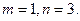
а) 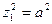- пара различных параллельных плоскостей.

б) 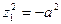- пара мнимых параллельных плоскостей.

в) 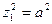- пара совпавших с плоскостью 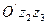плоскостей.

IV. 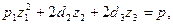где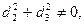

то есть d₂ и d₃ не равны нулю одновременно,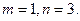

Разделим обе части этого уравнения на p₁ ≠0 и освободимся, как и в случае (3 ), от свободного члена p:

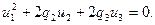
Обозначим 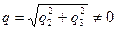и выполним ортогональное преобразование переменных (проверить!) по формулам:

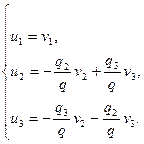
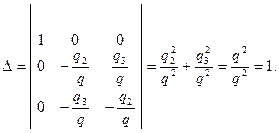
Оно означает переход к новой прямоугольной декартовой системе координат, относительно которой квадрика будет иметь уравнение:

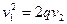– параболический цилиндр.

Замечание 2:подсчёт получившихся канонических или простейших уравнений показывает, что в пространстве E₃ существует семнадцать различных видов поверхностей 2-го порядка.