Определение 1: пусть даны овальная линия второго порядка ω с уравнением:
с11x12 + с22x22 + с33x32 + 2c12x1x2 + 2c13x1x3 + 2c23x2x3 = 0 (1)
к точке А (a1 : a2 : a3)R относительно некоторого R проективной плоскости P2 (не все cij=0, I,j=1,2,3).
Прямая a с уравнением
(с11a1 + с12a2+ с13a3)∙x1 + (с21a1 + с22a2+ с23a3)∙x2 + (с31a1 + с32a2+ с33a3)∙x3 = 0, (2)
где cij=cji называется полярой точки А относительно линии ω, а точка А называется полюсом прямой a относительно линии ω.
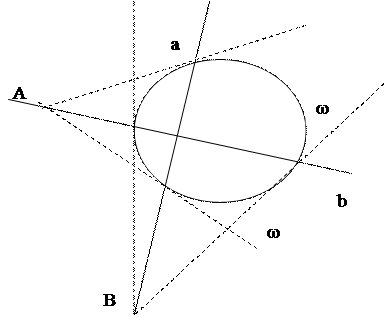
Теорема 1 (принцип взаимности): Если точка А лежит на поляре в точки В относительно овальной линии 2 – го порядка ω, то и точка В лежит на поляре а точки А:
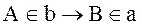
 |
Доказательство:
Если линия ω имеет уравнение (1), то поляра а точки А имеет уравнение (2), и поляра b точки В (b1: b2 : b3)R – уравнение:
(с11b1 + с12b2+ с13b3)∙x1 + (с21b1 + с22b2+ с23b3)∙x2 + (с31b1 + с32b2+ с33b3)∙x3 =0 (3)
По условию теоремы 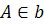 , следовательно, координаты точки А удовлетворяют уравнению (3):
, следовательно, координаты точки А удовлетворяют уравнению (3):
(с11b1 + с12b2+ с13b3)∙ a 1 + (с21b1 + с22b2+ с23b3)∙ a 2 + (с31b1 + с32b2+ с33b3)∙ a3 = 0
Сгруппируем члены с координатами b1, b2, b3 :
(с11a1 + с12a2+ с13a3)∙ b 1 + (с21a1 + с22a2+ с23a3)∙ b 2 + (с31a1 + с32a2+ с33a3)∙ b 3 = 0
Так как cij=cji, то координаты b1, b2, b3 точки В удовлетворяют уравнению (1), то если 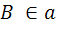 ▄
▄
Следствие: если на проективной плоскости Φ2 выбрана некоторая овальная линия второго порядка ω, то между точками и прямыми проективной плоскости Φ2 установлено взаимно-однозначное (объективное соответствие). При этом каждой точки соответствует определенная прямая – её поляра относительно ω, а каждой прямой определенная точка – её полюс относительно ω.
Это соответствие сохраняет взаимную принадлежность точки и прямой и называется полярным соответствием.
Остальные теоремы э того параграфа сформулируем без доказательств.
Теорема 2: Если точка лежит на овальной линии 2-го порядка, то её поляра является касательной к графику этой линии в этой точке.
 Способ построения этой касательной будет описан на практическом занятии (с помощью одной линейки)
Способ построения этой касательной будет описан на практическом занятии (с помощью одной линейки)
Теорема 3: Если точка А не лежит на овальной линии 2-го порядка ω, то её поляра а является множеством точек, гармонически сопряженных с точкой А относительно точек пересечения с линией ω всевозможных секущих, проходящих через точку А.
 |
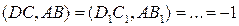 (4)
(4)
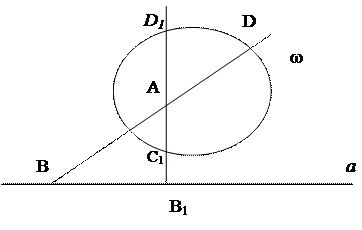
Теорема 4: Если точка А не лежит на овальной линии 2-го порядка ω, то её полярой а является диагональ полного четырехугольника, вписанного в ω, у которого точка А – диагональная точка, не лежащая на этой диагонали.

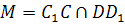
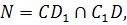
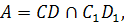
MN =a – поляра точки А относительно линии ω
M, N, A – диагональные точки полного четырехугольника СС1DD1 вписанного в овал ω
Пример 1: Построить поляру а точки А, не лежащей на данной овальной линии 2 порядка ω.
Способ 1: (основан на теореме 3).
Будем использовать чертеж к этой теореме.
Построение: 1) Проведем через точку А две произвольные секущие CD и C1D1
2) Строим на них точки B и B1 к точкам A, C, D и A1, C1, D1
(см. пример 1 из §14.)
3) a = BB1 – искомая поляра точки А.
Способ 2: (основан на теореме 4).
Будем использовать чертеж к этой теореме
Построение: 1) Проведем через точку А две произвольные секущие CD и C1D1;
2) Строим диагональ MN полного четырехвершинника CC1DD1: 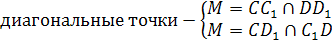
a=MN – искомая поляра точки А.
Способ 3: (основан на теоремах 1 и 2).
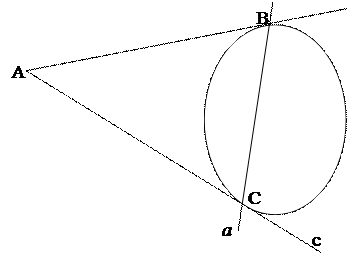
Случай 1: Точка А лежит вне овала ω:
1) Проведём через точку А две касательные b и c к овалу:
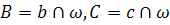
2) a= BC – искомая поляра точки А.
 |
Доказательство:
По теореме 2, касательные b и с к ω являются полярами точек B и С, так как 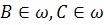 .
.
По теореме 1 (принцип взаимности):
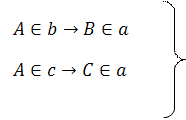
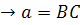
Случай 2: точка А лежит внутри овала 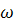 :
:
1. Проведем через точку А две секущие b и c к овалу  ;
;
2. Строим их полюсы B и C, как и в случай 1;
3. 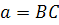 - искомая поляра точки А.
- искомая поляра точки А.
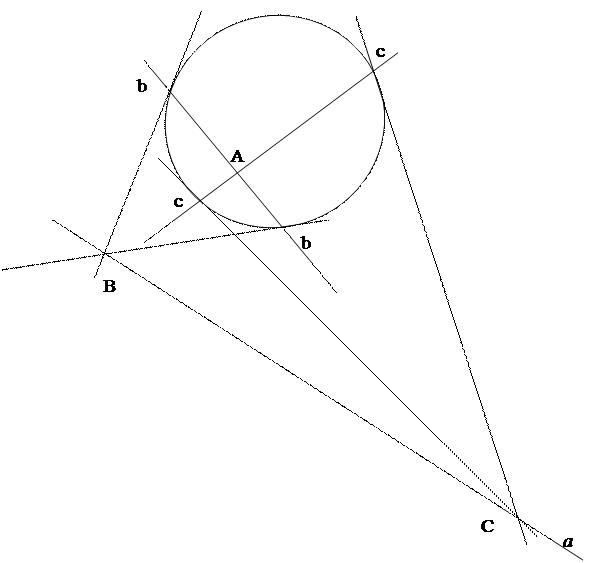
Доказательство проводится аналогично как и в случае 1.
Замечание: Касательные к овалу  строятся проектированием линейки к овалу в соответствующей точке, поэтому способ 3 является приближенным (прямая определяется однозначно двумя своими точками).
строятся проектированием линейки к овалу в соответствующей точке, поэтому способ 3 является приближенным (прямая определяется однозначно двумя своими точками).
Пример 2: Построить полюс А прямой а относительно данной овальной линии второго порядка 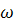 .
.
Построение (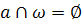 ) (см. рисунок к случаю 2).
) (см. рисунок к случаю 2).
1) Строим две произвольные точки B и C прямой a (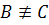 );
);
2) Строим поляры b и с точек B и C относительно овала B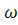 , эти поляры проходят через точки касания касательных к
, эти поляры проходят через точки касания касательных к 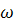 , проведенных из точек B и C;
, проведенных из точек B и C;
3) 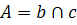 – искомый полюс прямой а.
– искомый полюс прямой а.
Доказательство:
Так как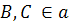 , то согласно принципу взаимности имеем:
, то согласно принципу взаимности имеем: 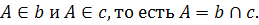 ▄
▄
 2014-02-24
2014-02-24 4626
4626








