Двойное отношение

II Основные факты проективной геометрии

Определение 1: Пусть A, B, C, D – четыре различные точки проективной прямой Р₁, порождающие их векторы 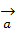, , 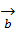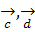связаны соотношениями:

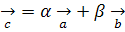
	(1)
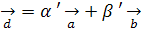
	(2)

Тогда двойственным или сложным отношением точек A, B, C, D называется число

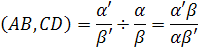
(3)

Замечание 1: (AB, CD)≠0 и (AB, CD)≠1.

1) Если 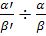=0, то 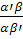=0 и либо 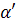=0, либо 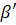=0. В случае 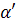=0 имеем 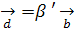и точки D и В совпадают (порождаются коллинеарными векторами). В случае 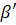=0 имеем 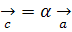и точки С и Ф совпадают. Точки же A, B, C, D предполагаются различными.

2) Если 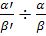=1, то =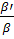, то есть векторы 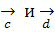коллинеарны и порождают одну точку, но С не совпадает с D.

Теорема 1: двойное отношение точек A(a₁:a₂)_R, B(b₁:b₂)_R, C(c₁:c₂)_R, D(d₁:d₂)_R, где R=(e₁;e₂;e) вычисляется по формуле:

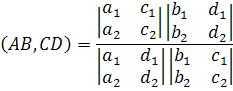
(4)

Доказательство:

Из соотношения (1) следует, что:

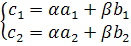
По формулам Крамера имеем:

, .

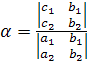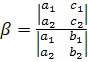Аналогично из соотношения (2) следует, что:

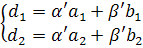
По формулам Крамера имеем:

, .

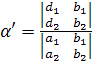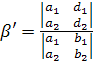Подставляя значения 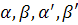в формулу (3), сокращая и переставляя столбцы в двух определителях, получаем искомую формулу (4).

Следствие 1:

а) двойное отношение не изменится, если в нем поменять местами пары точек:

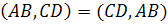
(5)

б) двойное отношение изменится на обратное, если поменять местами точки в одной из пар:

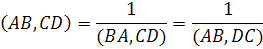
(6)

Доказательство:

Для проверки этих равенств достаточно каждое из двойных отношений выразить по формуле (4).

Следствие 2: двойное отношение четырех собственных точек A(a), B(b), C(c), D(d) расширенной евклидовой прямой 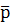выражается через их неоднородные координаты а, в, с, d по формуле:

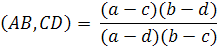
(7)

Доказательство:

По теореме из § 7 имеем: 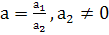(точка А – собственная).

Так как проективные координаты а₁ и а₂ точки А определены с точностью до общего множителя, то положив а₂=1, имеем а₁=а. Аналогично получаем 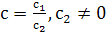. Если с₂=1, то с₁=с.

Отсюда: .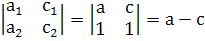

Заменяя определители в раенстве (4) указанным способом, приходим к равенству (7).

Определение 2: если 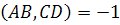, то четверка точек называется гармонической, пары точек A, B и C, D называются гармонически сопряженными, а точка D четвертой гармонической точкой к точкам А, В, С.

Теорема 2: на расширенной евклидовой прямой 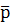середина отрезка гармонически сопряжена с несобственной точкой Р_∞ относительно его концов.

Доказательство:

Пусть С – середина отрезка АВ прямой 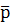и на ней введена неоднородная система координат О.

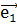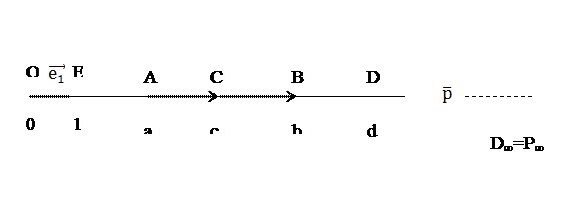
Тогда 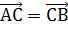и c-a=b-c, то есть .

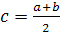Пусть теперь 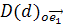– некоторая собственная точка прямой 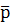. Тогда по следствию 2 из теоремы 1 имеем:

.

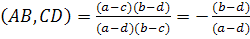Если устремить точку D к несобственной точке Р_∞, то d→∞ и окончательно получим:

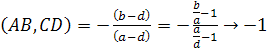при d→∞.

Итак, (АВ, СР_∞)= -1.

Теорема 3: 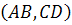<0 óA, B ÷ C, D – пары A, B и C, D разделяют друг друга.

Следствие: гармонически сопряженные пары точек разделяют друг друга: 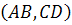= -1<0 => (A, B) ÷ (C, D).

Теорема 4: двойное отношение четырех точек прямой не меняется при проективном отображении, в частности при перспективном отображении (центральном проектировании). Обратно, всякое отображение прямой, сохраняющие двойное отношение любых четырех ее точек, является проективным отображением этой прямой.

Доказательство следует из определения проективного отображения и теоремы 1 (формула 4).

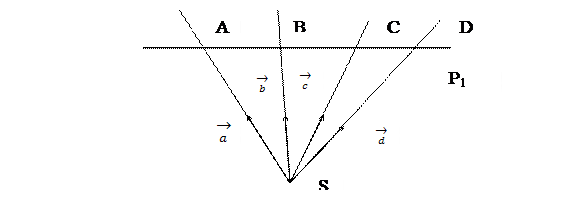
Определение 3: двойным или сложным отношением четырех прямых пучка называется двойное отношениечетырех точек, в которых эти прямые пересекаются с произвольной прямой р, не проходящей через центр пучка S: (ab, cd) = (AB, CD).

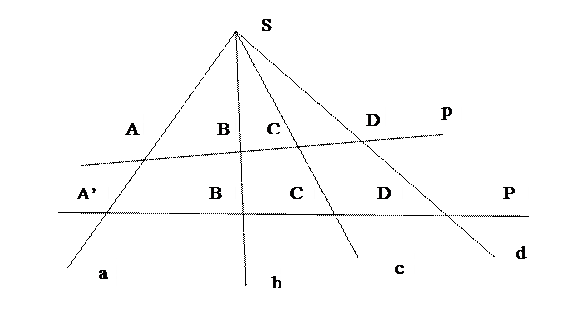
Замечание 2: согласно теореме 4, двойное отношение четырех прямых не зависит от выбора секущей прямой р: (ab, cd) = (AB, CD) = (A’B’, C’D’).

Теорема 5: 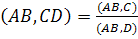– связь сложного отношения с простыми отношениями.