2014-02-24
2482
Определение 1: линией второго порядка или квадрикой на проективной плоскости Р2 называется множество точек М(х1: х2: х3), имеющее в некоторой проективной системе координат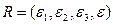 
уравнение вида:
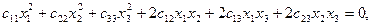(1)
где хотя бы один из коэффициентов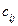 
отличен от нуля, и эти коэффициенты определены с точностью до числового множителя.
Замечание 1: формулы перехода от репера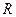 
к реперу 
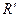на проективной плоскости 
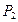имеют вид:
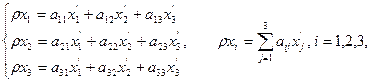(2)
где 
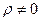и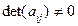 
.
Применяя их к уравнению (1), получим уравнение 2-ой степени относительно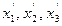 
, то есть уравнение такого же вида относительно «новых» проективных координат.
Поэтому понятие линии 2-го порядка на проективной плоскости не зависит от выбора проективной системы координат.
Имеет место следующая теорема:
Теорема 1: с помощью надлежащего выбора проективной системы координат уравнение (1) любой линии 2-го порядка на проективной плоскости может быть приведено к одному из следующих пяти видов:
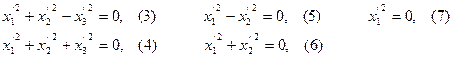
Определение 2: уравнения (3) – (7) называются нормальными уравнениями линии 2-го порядка.
Замечание 2: линия второго порядка на 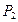с уравнением (3) называется овальной, ей принадлежит бесконечное множество точек.
Замечание 3: так как проективные координаты точки одновременно не могут равняться нулю, то уравнение (4) определяет пустое множество точек, а саму линию условно называют нулевой.
Замечание 4: уравнение (5) равносильно совокупности двух уравнени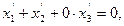й 
и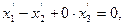 
поэтому говорят, что линия второго порядка распадается на пару прямых.
Замечание 5: уравнению (6) удовлетворяют координаты единственной точки (0:0:1), но поскольку из него следует, что л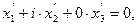ибо 
либо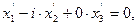 
где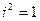 
, то линию с этим уравнением условно называют парой мнимых прямых, пересекаются в действительной точке (0:0:1).
Замечание 6: из уравнения (7) следует, что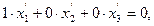 
поэтому говорят, что линия с этим уравнением является парой совпавших прямых.
Замечание 7: на евклидовой плоскости 
линией 2-го порядка было названо множество точек, имеющих в некоторой прямоугольной декартовой системе координат Oxy уравнение: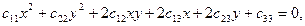 
где хотя бы один из старших коэффициентов не равен нулю.
Дополняя евклидову плоскость несобственной прямой и переходя к однородным аффинным координатам по формулам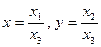 
, где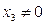 
для собственных точек, получаем уравнение:
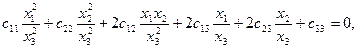
После умножения обеих его частей на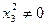 
, получаем уравнение (1), то есть уравнение линии 2-го порядка на проективной плоскости в проективных координатах.
В частности, эллипс, гипербола и парабола с точки зрения проективной геометрии являются овальными линиями 2-го порядка, а мнимый эллипс – нулевой линией.
Теорема 2: прямая на проективной плоскости 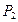может:
1) иметь с линией 2-го порядка две различные общие точки;
2) иметь с ней две совпавшие общие точки;
3) не иметь с ней общих точек;
4) целиком принадлежать линии 2-го порядка.
Определение 3: во втором случае прямая называется касательной к линии 2-го порядка.
Параметрические уравнения прямой на 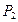имеют вид:
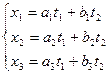, (8)
где параметры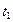 
и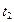 
определены с точностью до числового множителя, а прямая проходит через точк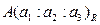и 
и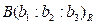 
. Положив 
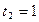подставив выражения для 
, 
, 
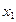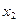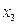в уравнение (1), получим уравнение вида
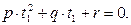(9)
Это уравнение может иметь два различных действительных корня, не иметь действительных корней и быть тождественным. Получаются четыре случая, описанные в условии теоремы. Подставляя значения 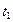из (9) и 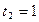в уравнения (8), найдем координаты точек пересечения. 
