Для последовательной цепи, состоящей из нескольких элементов, строится векторная диаграмма напряжений.
За исходный вектор принимается вектор тока, т.к. при последовательном соединении через все элементы цепи протекает один и тот же ток. Может быть показано, что напряжения на отдельных участках цепи сдвинуты по фазе относительно тока.
Пусть в цепи только активное сопротивление R.
По закону Ома ток в такой цепи 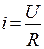
Т.к. U = Um cos ωt, то 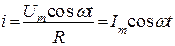 .
.
Отсюда следует, что напряжение и ток совпадают по фазе, а амплитуды тока и напряжения связаны законом Ома.
б) Пусть в цепи только индуктивность L.
Допустим, что ток в цепи i = Im cosωt.
Этот ток в индуктивности вызывает э.д.с. самоиндукции
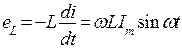 .
.
По 2-му закону Кирхгофа: eL = -uL,
отсюда получаем uL = – ωL Im sin ωt = UmL cos(ωt + π/2).
Из этого следует, что напряжение на индуктивности опережает ток на угол π/2, а амплитуды тока и напряжения можно то же связать законом Ома, если считать, что ωL=хL – индуктивное реактивное сопротивление
Рассуждая аналогично, для цепи с емкостью С выявим, что напряжение на емкости отстает от тока на угол π/2 (рекомендуется установить самостоятельно), а амплитуды тока и напряжение можно связать законом Ома, если считать 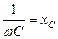 – реактивным емкостным сопротивлением.
– реактивным емкостным сопротивлением.
Таким образом, векторная диаграмма действующих значений напряжений для цепи с последовательно соединенными элементами R, L, C (см.рис.12) будет иметь вид, как показано на рис.13.
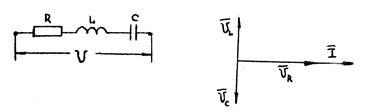
Рис.12 Рис. 13.
Вектор напряжения 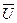 , приложенного к цепи, определяется как сумма векторов
, приложенного к цепи, определяется как сумма векторов 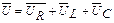 , а его величина равна
, а его величина равна
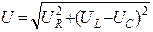
Для удобства восприятия взаимоотношений векторов, построим векторную диаграмму (рис. 15) напряжений для цепи, которая изображена на рис.14.
 ~ R1 L R2 C ~
~ R1 L R2 C ~

UR1 UL UR2 UC
U
Рис. 14
Для произвольных значений сопротивлений R, XL и XC и тока I она будет иметь вид, показанный на рис 15.
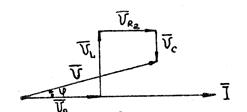 Рис. 15
Рис. 15
Вектор напряжения 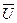 равен сумме векторов напряжений на отдельных участках цепи
равен сумме векторов напряжений на отдельных участках цепи
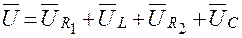 .
.
Если сумму векторов представить следующим образом:
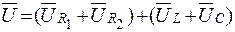 ,
,
то в соответствии с этой записью векторную диаграмму можно изобразить так, как показано на рис.16 или на рис.17.
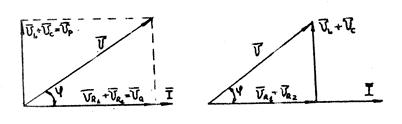
Рис. 16 Рис. 17
Векторная диаграмма, представленная на рис.17 называется треугольником напряжений. Вектор результирующего напряжения 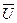 на рис.17 опережает вектор тока I на угол φ = ψu – ψi.
на рис.17 опережает вектор тока I на угол φ = ψu – ψi.
Если модули векторов треугольника напряжений разделить на модуль вектора тока, то получим сопротивления последовательной цепи R, X, Z:
R = R1 + R2; X = XL – XC 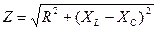
Эти сопротивления соотносятся как стороны прямоугольного треугольника. Прямоугольный треугольник, стороны которого численно равны величинам R, X, Z, называется треугольником сопротивлений (см. рис.18).
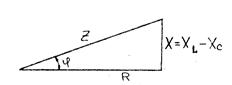
Рис. 18
Таким образом, 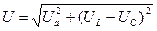 или
или 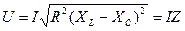 – это выражение является законом Ома для последовательной цепи переменного тока.
– это выражение является законом Ома для последовательной цепи переменного тока.
На рис. 15, 16, 17, 18 рассмотрен случай, когда XL>XC(UL>UC). Если ХL<XC, треугольники напряжений и сопротивлений будут иметь вид, показанный на рис.19 (а,б).

а) б)
Рис. 19
Обычно для расчета электрических цепей используют комплексные числа. Тогда все векторы можно изобразить на комплексной плоскости, как показано на рис.20 для цепи рис.14 (значения величин произвольные).
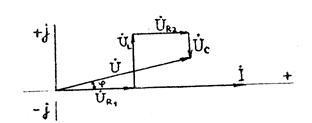 Рис.20
Рис.20
В комплексной форме полное напряжение записывается следующим образом
? =?а +?L +?C
Для цепи на рис.14
?a =?R1 +?R2, R = R1 + R2 ,
или? =?R + jωL? +? / jωC = (R + j (ωL – 1 / ωC))?.
Это соотношение есть закон Ома, записанный в комплексной форме. Сомножитель перед I есть полное сопротивление последовательной цепи в комплексной форме 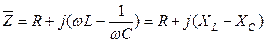 .
.
Полное комплексное напряжение  ? =
? = 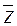 ?
?
В последовательной цепи возможен частный случай, когда XL=XC, при этом наступает режим, называемый резонансом напряжений. В этом случае ток в цепи максимальный. Большой ток, по закону Джоуля-Ленца, вызывает большие потери в проводах. В электроснабжении же всегда стоит задача снижения тока в подводящих проводах к приемнику. Те есть последовательный резонанс, с этой точки зрения, режим не экономичный.
Эту задачу можно решить, используя резонанс токов, который возникает в параллельной цепи, если в них содержатся реактивности с разным характером полей.
 2014-02-24
2014-02-24 22169
22169








