1. Графиком функции y = f(x) называется совокупность точек
координатной плоскости, координаты которых удовлетворяют
уравнению данной функции.
2. Графики часто встречающихся функций:
y = x y = –x

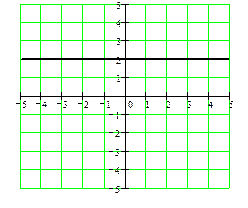
y = 2 x = 2

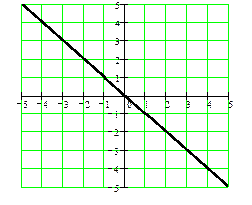
y = k∙x + b − прямая;
Прямую строим по двум точкам, придавая аргументу x два любых значения, а затем с помощью линейки проводим непосредственно прямую.
парабола квадратная парабола кубическая
y = x2 y = x3


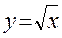 (полупарабола)
(полупарабола)
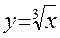

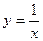 две гиперболы
две гиперболы 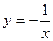
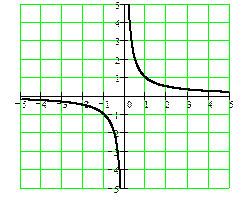
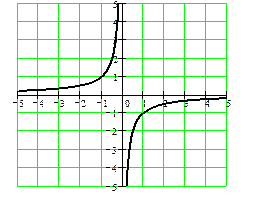
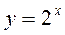 показательная функция
показательная функция 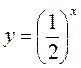
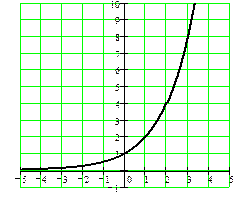
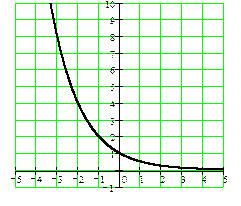
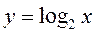
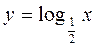
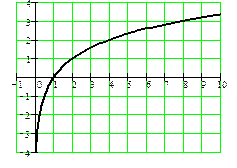

y = sin x
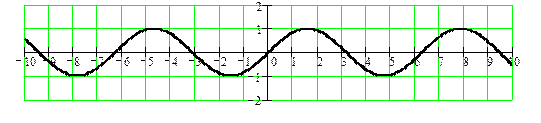
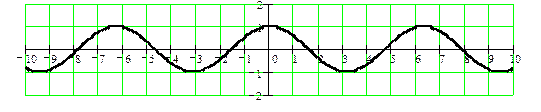
y = cos x
y = tg x
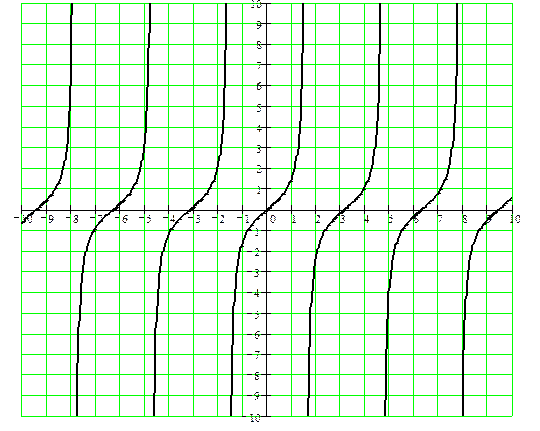
y = ctg x

y = sec x
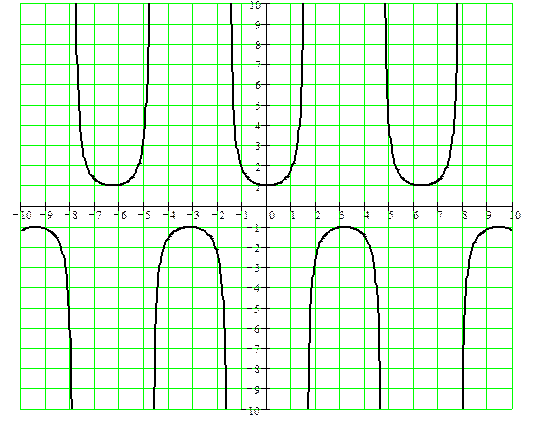
y = cosec x

y = arcsin x y = arccos x


−1 ≤ x ≤ 1 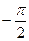 ≤ arcsin x ≤
≤ arcsin x ≤ 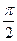 0 ≤ arcos x ≤ π
0 ≤ arcos x ≤ π
y = arctg x

y = arcctg x
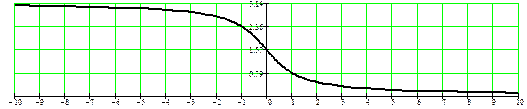
−∞ < x < +∞ 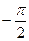 < arctg x <
< arctg x < 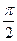 0 < arcctg x < π
0 < arcctg x < π
Функция “целая часть” или “антье”:
функцией антье (y = [x] или иногда y = a(x)) называется функция, принимающая для каждого значения x значение, равное наибольшему целому числу, не превосходящего этого x. Н а п р и м е р:
[1,2] = 1; [2,5] = 2; [4,87] = 4; [5] = 5;
[0] = 0; [−0,18] = −1; [−3,74] = −4; [−7] = −7;
y = [ x ]

Функция “дробная часть”: y = {x} = x – [x];
П р и м е р ы: {2} = 0; {−3} = 0;
{3,65} = 3,65 – [3,65] = 3,65 – 3 = 0,65;
{−2,37} = −2,37 – [−2,37] = −2,37 − (−3) = −2,37 + 3 = 0,63;
эта функция периодическая, основной период T = 1;
y = { x }

3. Преобразование графиков:
1) y = f(x) + c;
Пусть дан график функции y = f(x).
Тогда график функции y = f(x) + c получается из данного графика
путём его вертикального переноса вдоль оси oy:
вверх на c единиц при c > 0;
вниз на │ c │ единиц при c < 0;
2) y = f(x – a);
Горизонтальный перенос вдоль оси ox:
вправо на a единиц при a > 0;
влево на │ a│ единиц при a < 0;
3) y = −f(x); Переворот вокруг оси ox.
4) y = f(−x); Переворот вокруг оси oy.
5) y = k∙f(x); k > 0;
Точки пересечения с осью ox остаются прежними.
Растяжение вдоль оси oy в k раз при k > 1.
Сжатие вдоль оси oy в 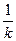 раз при 0 < k < 1.
раз при 0 < k < 1.
6) y = f(p∙x); p > 0;
Сжатие вдоль оси ox к оси oy в p раз при p > 1.
Растяжение вдоль оси ox от оси oy в 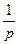 раз при 0 < p < 1.
раз при 0 < p < 1.
7) y = │f(x)│;
Части графика y = f(x), расположенные ниже оси ox, отобразить
симметрично вверх относительно оси ox. После этого части графика
y = f(x), расположенные ниже оси ox, отбросить.
8) y = f(│x│);
Строим график функции y = f(x) при x ≥ 0.
После этого симметрично отображаем его относительно оси oy.
Отбрасывать ничего не надо.
9) │y│ = f(x); (геометрическое место точек)
Строим сначала график функции y = f(x).
Части графика y = f(x), расположенные ниже оси ox, отбрасываем.
К оставшимся частям достраиваем их отражения симметрично
относительно оси ox. (одному значению x соответствует два
значения y).
10) │y − b│ = f(x); (геометрическое место точек)
Строим сначала график │y│ = f(x).
После этого вертикально его переносим вдоль оси oy:
вверх на b единиц при b > 0;
вниз на │ b │ единиц при b < 0;
4. График квадратного трёхчлена:
парабола y = a∙x2 + b∙x + c;
вершина параболы: точка A(x0, y0)
x0 = −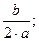
y0 = a∙x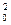 + b∙x
+ b∙x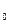 + c; (подставляем x0 в уравнение параболы)
+ c; (подставляем x0 в уравнение параболы)
направление ветвей параболы:
при a > 0 вверх;
при a < 0 вниз;
точка пересечения с осью oy: при x = 0 y = c;
точки пересечения с осью ox: корни x1 и x2;
5. График гиперболы 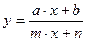 (обязательно должно быть m ≠ 0):
(обязательно должно быть m ≠ 0):
вертикальная асимптота: m∙x + n = 0; x = −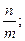
горизонтальная асимптота: y = 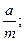
точка пересечения с осью oy: при x = 0 y = 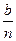 ; (при n ≠ 0)
; (при n ≠ 0)
если встречается случай n = 0, то гипербола не пересекает ось oy;
точка пересечения с осью ox: a∙x + b = 0; x = −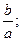 (при a ≠ 0)
(при a ≠ 0)
если a = 0, то гипербола не пересекает ось ox.
6. Окружность
а) уравнение: (x – a)2 + (y – b)2 = R2;
центр окружности находится в точке C(a; b).
радиус окружности равен R;
б) уравнение: x2 + y2 = R2;
центр окружности находится в точке O(0; 0).
радиус окружности равен R;
7. Асимптоты графика функции
а) горизонтальные асимптоты
прямая y = a является горизонтальной асимптотой кривой y = f(x),
если 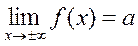 ;
;
б) вертикальные асимптоты
прямая x = a является вертикальной асимптотой кривой y = f(x),
если 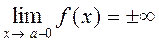 или
или 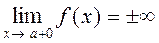 ;
;
в) наклонные асимптоты
если кривая y = f(x) имеет наклонную асимптоту y = k∙x + b, то
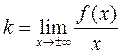 ;
;  ;
;
8. Чётность и нечётность функции (укр. парність або непарність)
Функция y = f(x) называется:
чётной, если f(−x) = f(x);
нечётной, если f(−x) = −f(x).
График чётной функции обладает осевой симметрией относительно
оси oy.
График нечётной функции обладает центральной симметрией
относительно начала координат (поворот на 180°).
Производная (укр. похідна)
1. Определение производной:
Производной данной функции y = f(x) по аргументу x называется
предел отношения приращения функции ∆y к приращению
аргумента ∆x, когда последнее произвольным образом стремится
к нулю, т.е. 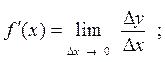
формула для приращения функции ∆y = f(x + ∆x) – f(x);
Обозначения производной:
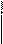 y '; y 'x; f '(x); f 'x(a); y ' = 5; y '(2) = 5;
y '; y 'x; f '(x); f 'x(a); y ' = 5; y '(2) = 5;
x = 2
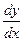 ;
; 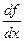 ;
; 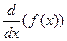 ;
;
y ''; y '''; yIV; yV; y(7); y(n);
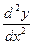 ;
; 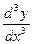 ;
; 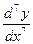 ;
; 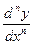 ;
;
Процесс нахождения производной называется дифференцированием.
2. Геометрическая интерпретация производной:
Тангенс угла наклона касательной, проведенной в точке дифферен −
цирования (угол отсчитывается от оси ox против часовой стрелки):
f '(x0) = tg α;

 y y = f(x)
y y = f(x)

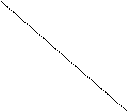
tg α1 > 0;

tg α2 < 0;
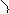
 α1 α2
α1 α2
 0 x0 x0 x
0 x0 x0 x
3. Таблица производных:
1) 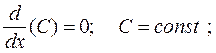
2) 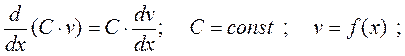
3) 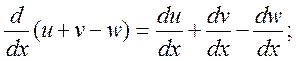
4) 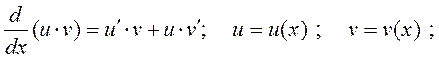
5) 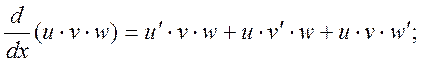
6) 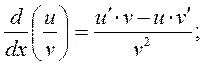
7) 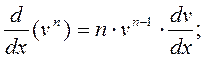
8) 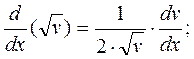
9) 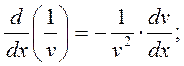
10) 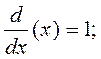
11) 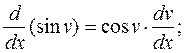
12) 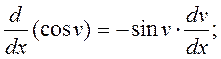
13) 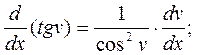
14) 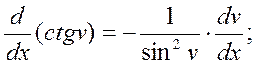
15) 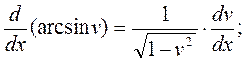
16) 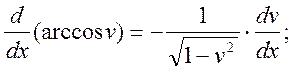
17) 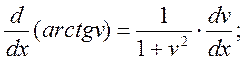
18) 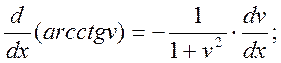
19) 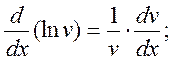
20) 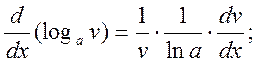
21) 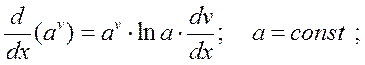
22) 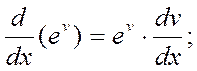
4. Вычисление дифференциала функции
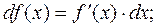 ∆y ≈ dy;
∆y ≈ dy;
(находим производную и умножаем на dx)
5. Приближённые вычисления с помощью дифференциала
f(x0 + ∆x) ≈ f(x0) + f '(x0)∙∆x;
6. Уравнение касательной
y – y0 = (x – x0)∙f '(x0);
y = f(x) − данная функция;
M(x0; y0) − точка касания;
7. Монотонность функции
возрастание при y ' > 0;
убывание при y ' < 0;
8. Экстремумы функции
а) критические точки: y ' = 0 или y ' не существует;
б) характер экстремума:
если при переходе слева направо производная меняет свой знак
с “+” на “−”, то функция имеет max в этой точке;
если при переходе слева направо производная меняет свой знак
с “−” на “+”, то функция имеет min в этой точке;
или
max при y ''(x0) < 0;
min при y ''(x0) > 0;
 9. Выпуклость, вогнутость и точки перегиба графика функции
9. Выпуклость, вогнутость и точки перегиба графика функции
 кривая выпукла при y '' < 0;
кривая выпукла при y '' < 0;
кривая вогнута при y '' > 0;
точки перегиба при y '' = 0 или когда y '' не существует
(точка перегиба A – это граница между
выпуклостью и вогнутостью графика функции, см. рисунок:)

 A
A
 °
°
10. Правило Лопиталя
(для раскрытия неопределённостей вида 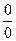 или
или 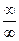 )
)
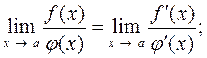
11. Производная в физике
S = S(t) − путь;
v = v(t) − скорость;
a = a(t) − ускорение;
t − время;
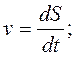
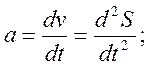
 2014-02-24
2014-02-24 5248
5248
