1 8 28 56 70 56 28 8 1
1 7 21 35 35 21 7 1
1 6 15 20 15 6 1
1 5 10 10 5 1
1 4 6 4 1
1 3 3 1
1 2 1
1 1
Разное
1. Формулы сокращённого умножения:
(a + b)2 = a2 + 2∙a∙b + b2;
(a − b)2 = a2 − 2∙a∙b + b2;
a2 − b2 = (a − b)∙(a + b);
(a + b)3 = a3 + 3∙a2∙b + 3∙a∙b2 + b3 = a3 + b3 + 3∙a∙b∙(a + b);
(a − b)3 = a3 − 3∙a2∙b + 3∙a∙b2 − b3 = a3 − b3 − 3∙a∙b∙(a − b);
a3 + b3 = (a + b)∙(a2 − a∙b + b2);
a3 − b3 = (a − b)∙(a2 + a∙b + b2);
2. Арифметическая прогрессия
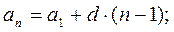
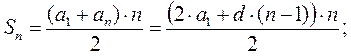
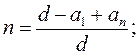
3. Геометрическая прогрессия
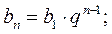
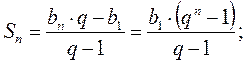
убывающая геометрическая прогрессия:
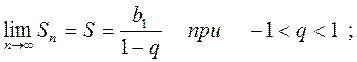
4. Наименьшие положительные периоды
y = A∙sin(a∙x + b); 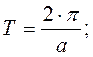
y = A∙cos(a∙x + b); 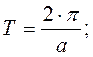
y = A∙tg(a∙x + b); 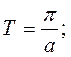
y = A∙ctg(a∙x + b); 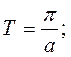
y = {x}; 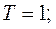
5. Теоремы о периодических функциях:
1) Если несколько периодических функций имеют один и тот же
период T, то сумма, произведение и частное этих функций также
периодические с тем же периодом T.
2) Периодом суммы, произведения и частного нескольких
периодических функций будет наименьшее общее кратное
периодов отдельных функций.
В случае суммы полученный период будет наименьшим
положительным.
В случае произведения или частного полученный результат
будет положительным периодом, но не всегда наименьшим.
6. Теорема Виета для кубического уравнения
x3 + p∙x2 + q∙x + f = 0;
x1 + x2 + x3 = −p;
x1∙x2 + x1∙x3 + x2∙x3 = q;
x1∙x2∙x3 = −f;
7. Решение диофантовых уравнений a∙x + b∙y = c,
где a, b, c – известные целые числа; x, y – неизвестные целые числа;
1) если a, b, c имеют общий множитель, то на него надо сократить
обе части уравнения;
2) коэффициенты a и b должны быть взаимно простыми, так как в
противном случае уравнение не имеет целых решений;
(числа называются взаимно простыми, если они не имеют
общих делителей)
3) находим любое целочисленное решение данного уравнения
x = x0 и y = y0.
Тогда общие решения имеют вид:
x = x0 − b∙n;
y = y0 + a∙n;
где n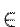 Z, т.е. n – любое целое число;
Z, т.е. n – любое целое число;
8. Рациональные корни уравнения
Теорема: если рациональное число 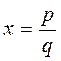 является корнем
является корнем
алгебраического уравнения с целыми коэффициентами
a0∙xn + a1∙xn-1 + a2∙xn-2 + … + an-1∙x + an = 0, то
p является делителем свободного члена an;
q является делителем старшего коэффициента a0;
9. Схема Горнера
предназначена для деление многочлена на разность (x – a)
1) 3∙x4 − 2∙x3 + x – 4 на (x – 2) (a = 2)
 3 3
| −2 |
| |||||
 2 2
|  30 30
|

умножаем слева направо и прибавляем сверху;
Вывод: 3∙x4 − 2∙x3 + x – 4 = (x – 2)∙(3∙x3 + 4∙x2 + 8∙x + 17) + 30;
2) 5∙x4 + 11∙x3 − 13∙x2 − 8∙x − 15 на (x + 3) (a = −3, т.к. x + 3 = x−(−3))
 5 5
| −13 | −8 | −15 | ||
 −3 −3
| −4 | −1 | −5 |
Вывод: 5∙x4 + 11∙x3 − 13∙x2 − 8∙x – 15 = (x + 3)∙(5∙x3 − 4∙x2 – x − 5);
10. Разложение многочлена по степеням (x – a) при помощи
схемы Горнера
разложить P(x) = 5∙x4 − 3∙x2 + 4∙x + 2 по степеням (x + 2)
 5 5
| −3 | ||||
| −2 | −10 | −30 | |||
| −2 | −20 | −144 | |||
| −2 | −30 | ||||
| −2 | −40 | ||||
| −2 |
Ответ: P(x) = 5∙(x + 2)4 − 40∙(x + 2)3 + 117∙(x + 2)2 − 144∙(x + 2) + 62;
11. Соединения и бином Ньютона
факториал n! = 1 ∙ 2 ∙ 3 ∙ 4 ∙…∙ (n − 2)∙(n − 1)∙n;
размещения 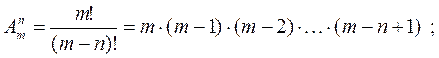
перестановки 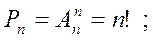
сочетания 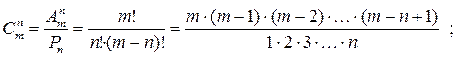
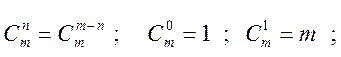 во всех формулах n ≤ m;
во всех формулах n ≤ m;
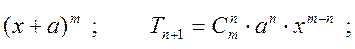
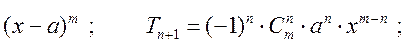
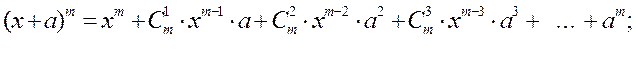
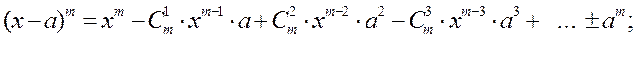
Треугольник Паскаля (биномиальные коэффициенты)
и т. д.
12. Производные пропорции
Если 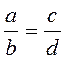 , то:
, то:
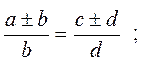
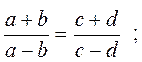
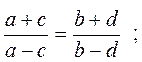
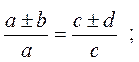
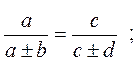
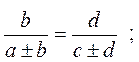
 2014-02-24
2014-02-24 492
492








