1. Правильный (равносторонний) треугольник
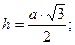
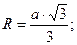
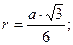
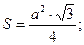
2. Равнобедренный треугольник
a – основание; b – боковая сторона;
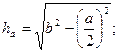
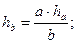
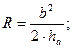
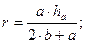
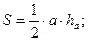
3. Прямоугольный треугольник
a и b – катеты; c – гипотенуза;
теорема Пифагора: a2 + b2 = c2;
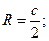
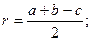
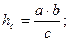
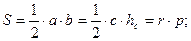
 | |||
 | |||
h2 = m∙n; метрические
m a2 = (m+n)∙m; соотношения
 a b2 = (m+n)∙n; в прямоугольном
a b2 = (m+n)∙n; в прямоугольном
h n 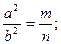 треугольнике
треугольнике
 b
b
тригонометрические функции острого угла:


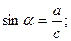
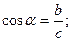
c a 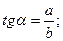
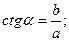
 α
α

b
4. Произвольный треугольник
формула Герона 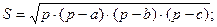
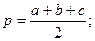
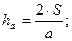
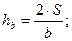
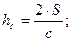
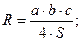
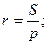
медиана 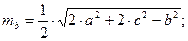
биссектриса 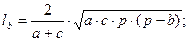



α
b c 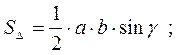

 γ β
γ β
a
теорема синусов: 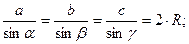
теорема косинусов: a2 = b2 + c2 − 2∙b∙c∙cos α;
теорема тангенсов: 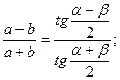
Средняя линия любого треугольника параллельна основанию и равна его
половине.
Число диагоналей выпуклого n-угольника 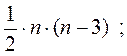
5. Точки в произвольном треугольнике:
а) центр вписанного круга лежит в точке пересечения биссектрис;
б) центр описанного круга лежит в точке пересечения серединных
перпендикуляров к сторонам;
в) точка пересечения медиан отсекает от каждой медианы ее третью
часть;
г) высоты пересекаются в одной точке, называемой ортоцентром
треугольника.
6. Треугольники подобны, если в них равны по два угла.

 7. Свойство биссектрисы любого треугольника
7. Свойство биссектрисы любого треугольника

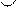
α α
a b 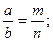

m n
8. Квадрат
 A B AB = BC = CD = AD = a;
A B AB = BC = CD = AD = a;
d AC = d;
a a d = a∙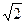 ;
;
D C
9. Углы со взаимно параллельными или взаимно перпендикулярными
сторонами равны.
10. Трапеция
средняя линия 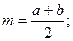
площадь 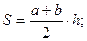
11. Параллелограмм
площадь S = a∙h = a∙b∙sin α;
Сумма квадратов диагоналей равна сумме квадратов его сторон.
12. Площадь выпуклого 4-х угольника равна половине произведения его
диагоналей на синус угла между ними:
S = 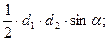
13. Сумма внутренних углов выпуклого n-угольника равна 180°∙(n−2);
А сумма внешних углов выпуклого n-угольника равна 360°;
14. Круг
площадь S = π∙R2; длина окружности C = 2∙π∙R;
длина дуги 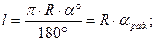
площадь сектора 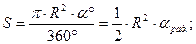
площадь сегмента 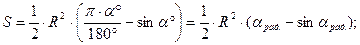
 15. Пересекающиеся хорды в круге
15. Пересекающиеся хорды в круге
 A AK∙KB = CK∙KD;
A AK∙KB = CK∙KD;
 K D
K D
C B
16. Касательная и секущая к окружности


 A B Если из одной точки к окружности
A B Если из одной точки к окружности
проведены касательная и секущая, то
C квадрат касательной равен произведению
секущей на её внешнюю часть:
D AB2 = BD∙BC;
17. Угол, вписанный в окружность, измеряется половиной дуги, на
которую он опирается.
18. Если в 4-х угольник произвольной формы вписана окружность, то
суммы противоположных сторон этого 4-х угольника равны.
 b
b
 a + c = b + d;
a + c = b + d;
a c
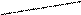
d
19. Если в окружность вписан 4-х угольник произвольной формы, то
суммы противоположных углов этого 4-х угольника равны и равны
180°, т.е. 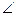 A +
A + 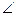 C =
C = 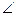 B +
B +  D = 180°;
D = 180°;
 Кроме того, справедлива теорема Птолемея:
Кроме того, справедлива теорема Птолемея:
 A В 4-х угольнике, вписанном в круг,
A В 4-х угольнике, вписанном в круг,

 B произведение диагоналей равно
B произведение диагоналей равно
 D сумме произведений противоположных
D сумме произведений противоположных
C сторон, т.е. AC∙BD = AB∙CD + BC∙AD;
20. Касательные, проведенные к окружности из одной точки, равны.
 |
 2014-02-24
2014-02-24 657
657








