Министерство образования Российской Федерации
Хабаровская государственная академия экономики и права
Кафедра математики и математических методов в экономике
Высшая математика
Приложения производной к исследованию функций
Методические указания и индивидуальные задания для
Студентов 1-го курса дневного отделения
Всех специальностей
Хабаровск 2003
ББК В11
Х12
Высшая математика. Приложения производной к исследованию функций: Методические указания и индивидуальные задания для студентов 1-го курса дневного отделения всех специальностей / Сост. И.В. Ясеновская – Хабаровск: РИЦ ХГАЭП, 2003. – с. 32
Рецензент к.ф.-м.н., доцент кафедры прикладной математики ДВГУПС Е.Н. Ломакина
Методическая разработка предназначена для выполнения индивидуальных заданий по высшей математике для студентов первого курса всех специальностей дневного отделения.
Задания предусматриваются по следующими темам: «Исследование функций и построение графиков», «Исследование функций на наименьшее и наибольшее значения», «Приближенные вычисления с помощью дифференциала» и «Экономический смысл производной».
Структура методических указаний следующая: дана подробная схема исследования функции, рассмотрено решение типовых задач, составлены варианты заданий для самостоятельного решения. При подборе упражнений использовалась различная учебная литература. Основные понятия изучаемого раздела иллюстрируются задачами экономического содержания.
Утверждено издательско-библиотечным советом академии в качестве методических указаний.
© Хабаровская государственная академия экономики и права, 2003
ИССЛЕДОВАНИЕ ФУНКЦИЙ ОДНОЙ
ПЕРЕМЕННОЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ И ПОСТРОЕНИЕ ГРАФИКОВ
Дифференциальное исчисление позволяет установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление выпуклости и вогнутости графика, наличие асимптот. Характерные точки – точки разрыва, экстремума, перегиба, пересечения графиков с осями координат служат опорными точками при исследовании функций и построении их графиков.
При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность–нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Заметим, что исследование функции проводится одновременно с построением ее графика.
Пример 1. Исследовать функцию и построить ее график
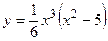 .
.
Решение
1. Очевидно, что функция определена на интервале х 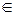 (-
(- 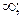 +
+ 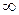 ).
).
2. Функция нечетная, так как 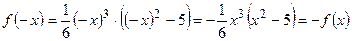 .
.
Следовательно, ее график симметричен относительно начала координат.
3. Так как функция непрерывна на всей области определения, то точек разрыва она не имеет, а следовательно, не имеет и вертикальных асимптот.
4. Наклонная асимптота имеет вид 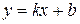 , если существуют конечные пределы
, если существуют конечные пределы
k = 
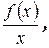 b =
b = 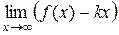 .
.
Найдем эти пределы для данной функции:
k = 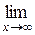
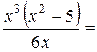
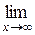
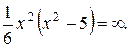
Таким образом, функция не имеет ни наклонных, ни горизонтальных асимптот.
5. Очевидно, что 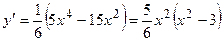 .
.
Приравняем производную к нулю.
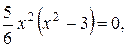
имеем три критические точки: х 1=0, х 2= 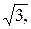 х 3= -
х 3= - 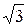 .
.
Всю область определения разобьем на следующие три промежутка:
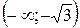 ,
, 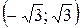 ,
, 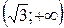

На каждом из этих промежутков устанавливаем знак производной.
Очевидно, что 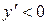 на промежутке
на промежутке 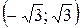 , и
, и 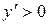 на промежутках
на промежутках 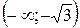 и
и 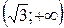 . Следовательно, на
. Следовательно, на 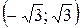 функция
функция 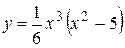 убывает, на
убывает, на 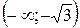 и
и 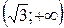 - возрастает.
- возрастает.
Таким образом, определены промежутки монотонности. В точке 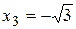 функция имеет максимум. В точке
функция имеет максимум. В точке 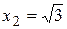 функция имеет минимум,
функция имеет минимум, 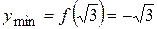 ;
; 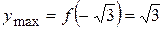 . Обозначим полученные точки: А
. Обозначим полученные точки: А 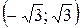 - max; B
- max; B 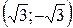 - min.
- min.
6. Найдем
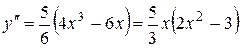 .
.
Приравняем вторую производную к нулю.
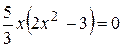 .
.
Корни этого уравнения следующие:
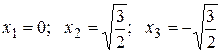 .
.
Всю область определения функции разобьем на промежутки:
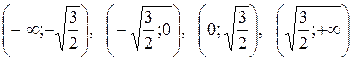 .
.
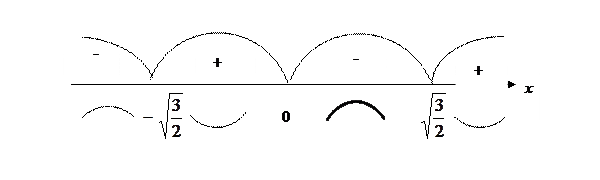
Следовательно, на промежутках 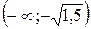 и
и 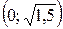 функция выпукла (выпукла вверх), а на промежутках
функция выпукла (выпукла вверх), а на промежутках 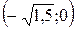 и
и 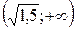 - вогнута (выпукла вниз).
- вогнута (выпукла вниз).
Так как вторая производная при переходе через точки 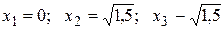 меняет знак, то все эти точки являются абсциссами точек перегиба. Находим их ординаты:
меняет знак, то все эти точки являются абсциссами точек перегиба. Находим их ординаты:
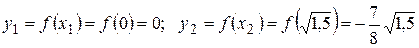 ;
;
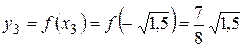 .
.
Таким образом, точками перегиба являются следующие точки:
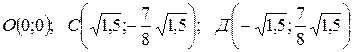 .
.
7. Найдем точку пересечения графика функции с осью Оу. Тогда при х = 0 получаем из уравнения 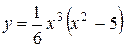 , что и у = 0. Итак, ось Оу график функции пересекает в точке О(0;0).
, что и у = 0. Итак, ось Оу график функции пересекает в точке О(0;0).
Для нахождения точек пересечения графика с осью Ох решим уравнение 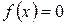 .
.
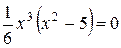 .
.
Отсюда получаем х = 0; 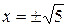 . Тогда график функции пересекает ось Ох в трех точках О(0;0); Е
. Тогда график функции пересекает ось Ох в трех точках О(0;0); Е 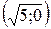 ; F
; F 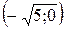 .
.
График функции изображен на рис. 1.
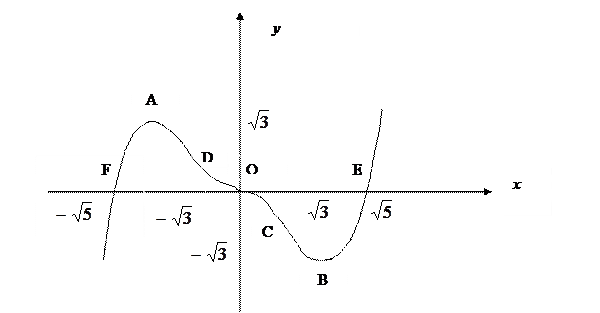
Рис.1. График функции 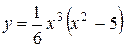 .
.
Пример 2. Исследовать функцию и построить её график
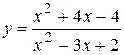 .
.
Решение
1. Найдем область определения функции. Для этого необходимо решить квадратное уравнение
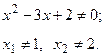
Следовательно, область определения функции 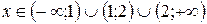 .
.
2. Исследуем функцию на четность и нечетность
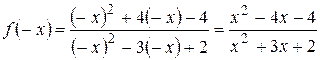 .
.
Очевидно, что данная функция не является ни четной ни нечетной.
3. Проведем классификацию точек 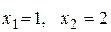 разрыва функции. Для этого вычислим правосторонние и левосторонние пределы в точках разрыва.
разрыва функции. Для этого вычислим правосторонние и левосторонние пределы в точках разрыва.
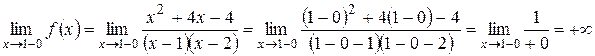
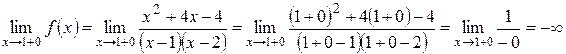
Аналогично получаем 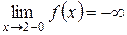 ;
; 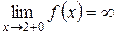 .
.
Следовательно, точки 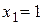 и
и 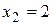 являются точками разрыва второго рода, а прямые х = 1 и х = 2 – вертикальными асимптотами графика функции.
являются точками разрыва второго рода, а прямые х = 1 и х = 2 – вертикальными асимптотами графика функции.
4. Найдем наклонную асимптоту графика функции
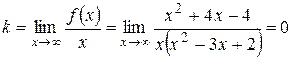 ;
;
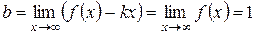 .
.
Следовательно, горизонтальная асимптота у = 1 явилась частным случаем наклонной асимптоты.
5. Найдем производную данной функции
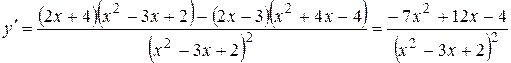 .
.
Таким образом, первая производная не существует в точках разрыва функции 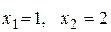 . Решая уравнение
. Решая уравнение 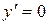 ,
, 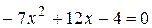 , получим
, получим 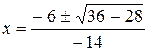 ,
, 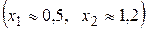 .
.
Наносим критические точки на числовую прямую.
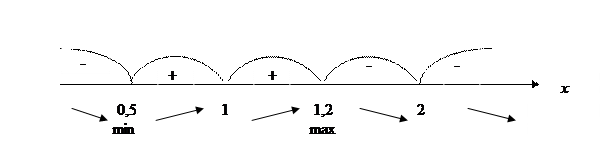
Очевидно, что 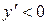 на промежутках
на промежутках 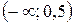 ;
; 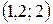 и
и 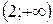 , на этих промежутках функция убывает. На промежутках, где
, на этих промежутках функция убывает. На промежутках, где 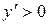 - (0,5;1), (1;1,2) функция возрастает.
- (0,5;1), (1;1,2) функция возрастает.
Соответственно точками экстремума являются точки с абсциссами х 1 = 0,5 – минимум и х 2 = 1,2 – максимум. Таким образом, у min= f(0,5) = -2,5 и у max=f(1,2) = -10.
Обозначим полученные точки А(0,5; -2,5) – min и В(1,2; -10) – max.
6. Исследуем функцию на наличие точек перегиба.
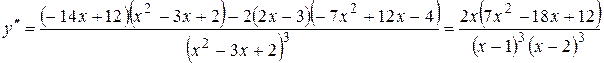
Вторая производная существует на  , (1;2),
, (1;2), 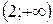 .
.
Найдем точки, подозрительные на перегиб, для этого решим уравнение
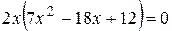 .
.
Получим х =0; так как D<0, то 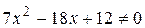 .
.
Нанесем точки на ось
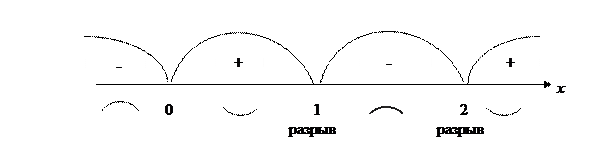
Таким образом, на промежутках 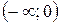 и (1; 2) – функция выпукла (выпукла вверх), а на промежутках (0; 1) и
и (1; 2) – функция выпукла (выпукла вверх), а на промежутках (0; 1) и 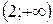 - вогнута (выпукла вниз).
- вогнута (выпукла вниз).
Для точки с абсциссой х = 0 найдем её ординату 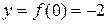 .
.
Таким образом, график функции имеет единственную точку перегиба С(0;-2).
7. Найдем точку пересечения графика функции с осью Оу. При х = 0, у = -2. Точка С(0;-2) – точка пересечения с Оу.
Для нахождения точек пересечения графика с осью Ох решим уравнение
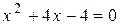 .
.
Получаем 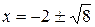 . Следовательно,
. Следовательно, 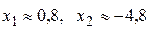 .
.
Назовем точки пересечения графика с осью Ох Д(0,8; 0) и Е(-4,8; 0).
График функции изображен на рис. 2.
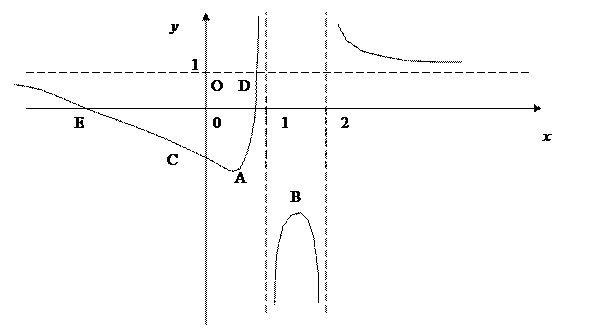 Рис. 2. График функции
Рис. 2. График функции 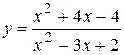 .
.
Пример 3. Исследовать функцию и построить её график
 .
.
Решение
1. Данная функция определена в области определения функции 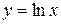 . По определению логарифма получаем
. По определению логарифма получаем 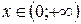 .
.
2. Функция не является ни четной ни нечетной.
3. Так как 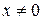 , то у функции имеется точка разрыва х = 0.
, то у функции имеется точка разрыва х = 0.
Определим вид точки разрыва. Поскольку область определения функции х >0, рассмотрим правосторонний предел
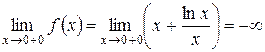 .
.
Следовательно, точка х = 0 – точка разрыва второго рода. Соответственно график функции имеет вертикальную асимптоту с уравнением х = 0.
4. Проверим функцию на наличие наклонных асимптот с уравнением 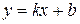 , где
, где
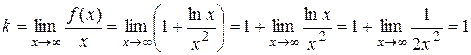 ;
;
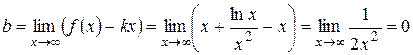 .
.
Получаем уравнение наклонной асимптоты у = х.
5. Исследуем функцию на монотонность.
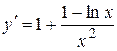 .
.
Приравняем производную к нулю.
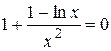 .
.
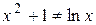 .
.
Учитывая, что производная на промежутке 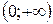 всегда положительна, сделаем вывод, что функция на этом промежутке монотонно возрастает.
всегда положительна, сделаем вывод, что функция на этом промежутке монотонно возрастает.
6. Найдем вторую производную функции
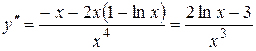 .
.
Решаем уравнение  , т.е.
, т.е. 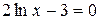 ,
,
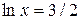 ,
,
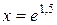 .
.
Исследуем полученную точку на перегиб
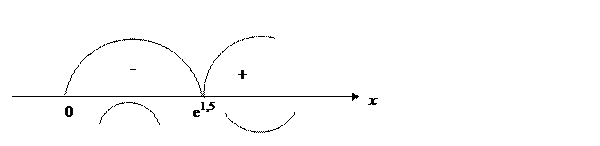
Действительно, на промежутке (0; е1,5) функция выпукла, а на промежутке (е1,5;+∞) – вогнута. Следовательно, точка с данной абсциссой является точкой перегиба функции.
Найдем её ординату 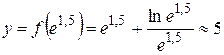 .
.
Таким образом, получим точку А(е1,5; 5).
7. В силу того, что 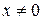 , график функции
, график функции 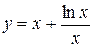 не имеет точек пересечения с осью Оу.
не имеет точек пересечения с осью Оу.
Определим точки пересечения функции с осью Ох. Для этого необходимо решить уравнение 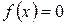 .
.
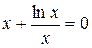 ,
,
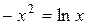 .
.
Решим это уравнение графически. Построим в прямоугольной системе координат графики функций 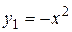 и
и 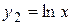 .
.

Получили точку К, абсцисса этой точки  , поэтому искомая точка пересечения графика функции
, поэтому искомая точка пересечения графика функции 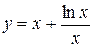 с осью Ох будет иметь координаты (0,6; 0), обозначим эту точку В(0,6; 0).
с осью Ох будет иметь координаты (0,6; 0), обозначим эту точку В(0,6; 0).
|
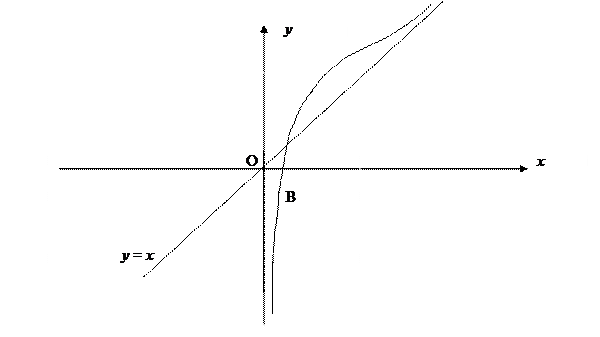
Рис. 3. График функции 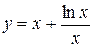 .
.
 2015-07-14
2015-07-14 2027
2027







