Явление Гиббса

Можно было бы ожидать, что отклонение между идеальным ФНЧ и рассчитанным тем незначительнее, чем больше коэффициентов было учтено в последнем. Это предположение соответствует действительности для суммы отклонений, но не для каждой разности.

В передаточной функции аппроксимирующего фильтра есть постоянные выбросы, составляющие 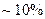. Амплитуда выбросов независима от количества коэффициентов фильтра. При возрастании 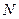отклонение только приближается к фронту импульса фильтра. Такое явление называется явлением Гиббса.

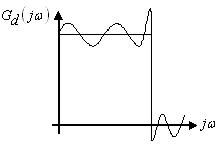
Рис 7. Явление Гиббса.

Функции окна. Выбросы в передаточной характеристике ФНЧ объясняются скачком идеальной передаточной ПФ-функции при .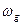

Благодаря применению функции окна w(t) эти выбросы можно ограничить за счет крутизны фронта ПФ-функции. Уравнение фильтра имеет вид:

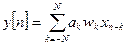, (1)

а передаточная характеристика:

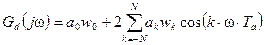. (2)

В качестве сглаживающих функций подходят колоколообразные функции. Например, функция окна фон Хана:

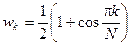. (3)

Пример:

Для фильтра низких частот при 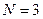получим коэффициенты сглаживания:

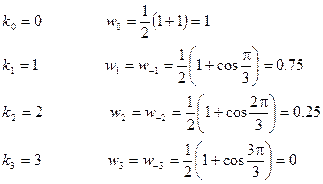
Замечание:

Частота дискретизации при нерекурсивных ФНЧ должна немного превышать граничную. Приемлемыми являются коэффициенты от 4 до 6. Наличие большой частоты не очень приемлемо (требуемая передаточная функция будет недостаточно приближена).

Лекция №7. Расчет коэффициентов для высокочастотных,

полосовых и режекторных фильтров.