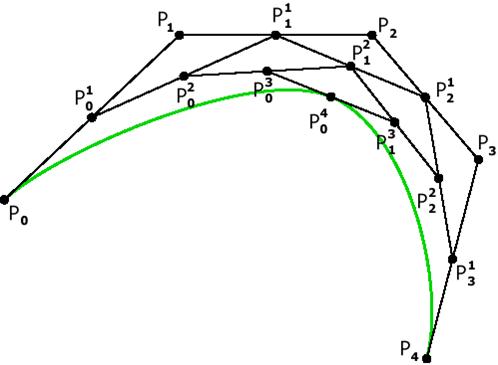
 Рис. 10. Построение кривой Безье методом разбиения.
Рис. 10. Построение кривой Безье методом разбиения.
| Предложен de Casteljau.
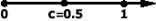 Если рассмотреть участок между
Если рассмотреть участок между  и и  , взятых для t=0,5, то он может быть задан как кривая Безье с опорными точками , взятых для t=0,5, то он может быть задан как кривая Безье с опорными точками 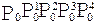 , аналогичные рассуждения справедливы и для участка между , аналогичные рассуждения справедливы и для участка между 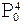 и и 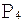 . Таким образом будем применять этот алгоритм рекурсивно для левой и правой частей, пока размер кривой не станет меньше размера пиксела. . Таким образом будем применять этот алгоритм рекурсивно для левой и правой частей, пока размер кривой не станет меньше размера пиксела.
|
Алгоритм:
PutPixel(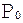 );
);
PutPixel(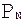 );
);
DrawCurve (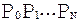 )
)
{
// Проверка на завершение
if (BBox(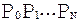 ) < pixelsize) return;
) < pixelsize) return;
if (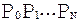 - прямая линия с точностью до пиксела)
- прямая линия с точностью до пиксела)
{
Нарисовать эту линию;
return;
}
Найти 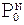 ;
;
PutPixel(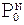 );
);
// Нарисовать половинки
DrawCurve(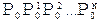 );
);
DrawCurve(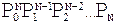 );
);
}
 2014-02-24
2014-02-24 417
417








